Question

在OACB中,BD=BC,OD与BA相交于E.求证：BE=BA.

Answer 1

思路分析：由已知条件可知O、E、D三点共线,点B、E、A也共线,再以边OA、OB对应的向量为基底,寻找出图中有关向量与基底的关系,从而达到证题的目的.

证法一：设E′是线段BA上的一点,且BE′=BA,只要证E、E′重合即可.

设=a, =b,则=a,OD?=b+a.

∵,,,

∴=(a+3b)= (b+a).

∴.

∴O、E′、D三点共线.

∴BE=BA.

证法二：设=a,=b,则=a,=b+a.

∵O、E、D三点共线,

∴,共线.

∴=λ(b+a).

又∵点B、E、A也共线,则,共线.

∴=μ(a-b).

∴=b+μ(a-b)=μa+(1-μ)b.

∴λ(b+a)=μa+(1-μ)b.

由a、b不共线,可得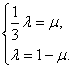

解得μ=.∴.∴BE=BA.

方法归纳 利用向量证明平面几何问题的关键是选好一组与所求证的结论密切相关的基底,其中一组基底是指平面内的两个不共线的向量.