题目内容
【题目】已知椭圆 
+ 
=1两焦点分别为F1、F2 ， P是椭圆在第一象限弧上一点，并满足 
=1，过P作两条直线PA、PB分别交椭圆于A、B两点．
（1）求P点坐标；
（2）若直线AB的斜率为 
，求△PAB面积的最大值．
【答案】
（1）解：由题意得：c= 
，则F1（0， ），F2（0，﹣ ），设P（x0，y0）
则 
=（﹣x0， ﹣y0）， 
=（﹣x0，﹣ ﹣y0），
由 =1，得：x02﹣2+y02=1x02+y02=3
又2x02+y02=4，x0，y0＞0，
∴ 
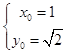，即所求P（1， ）
（2）解：设AB方程为：y= 
+m，由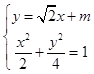 
，可得4x2+2 
mx+m2﹣4=0，△=8m2﹣18m2+64＞0，解得﹣2 
，设A（x1，y1），B（x2，y2），x1+x2= 
，x1x2= 
，
|AB|= 
= 
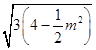．P到AB的距离为d= 
，
则 
= 
= 
= 
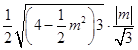当且仅当m=±2∈（﹣2 
）时取得最大值．
△PAB面积的最大值为：
【解析】（1）设出P的坐标，则可分别表示出向量，通过向量的数量积，求得x0和y0的关系，同时根据椭圆的方程，求得x0和y0即P的坐标．（2）设出直线的方程联立椭圆方程，可求出AB的距离，得到直线AB的距离，利用三角形的面积公式，通过基本不等式求解最值即可．
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案【题目】已知抛物线C：y2=8x的焦点为F，准线l与x轴的交点为M，过点M的直线l′与抛物线C的交点为P，Q，延长PF交抛物线C于点A，延长QF交抛物线C于点B，若 
+ 
=22，则直线l′的方程为 ．
【题目】由于雾霾日趋严重，政府号召市民乘公交出行．但公交车的数量太多会造成资源的浪费，太少又难以满足乘客需求．为此，某市公交公司在某站台的60名候车乘客中进行随机抽样，共抽取10人进行调查反馈，所选乘客情况如下表所示：
组别 | 候车时间（单位：min） | 人数 |
一 | [0，5） | 1 |
二 | [5，10） | 5 |
三 | [10，15） | 3 |
四 | [15，20） | 1 |
（1）估计这60名乘客中候车时间少于10分钟的人数；
（2）现从这10人中随机取3人，求至少有一人来自第二组的概率；
（3）现从这10人中随机抽取3人进行问卷调查，设这3个人共来自X个组，求X的分布列及数学期望．
