题目内容
已知数列{an}满足an=31-6n，数列{bn}满足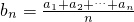
，则数列{|bn|}的前20项之和为：
- A.187
- B.164
- C.257
- D.304
D
分析：现根据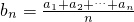求出{bn}的通项公式，然后再根据等差数列的前n项和公式进行求解即可得到答案．
解答：由an=31-6n得，{an}是一个以25为首项，公差为-6的等差数列．
所以
=28-3n
由bn=28-3n＞0得，
，
所以当1≤n≤9时，|bn|=28-3n，
当10≤n≤20时，|bn|=3n-28
所以数列{|bn|}的前20项之和
故答案为：D
点评：本题主要考查等差数列求和的前n项公式．考查学生的运算能力．
分析：现根据
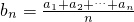求出{bn}的通项公式，然后再根据等差数列的前n项和公式进行求解即可得到答案．解答：由an=31-6n得，{an}是一个以25为首项，公差为-6的等差数列．
所以
=28-3n由bn=28-3n＞0得，
，所以当1≤n≤9时，|bn|=28-3n，
当10≤n≤20时，|bn|=3n-28
所以数列{|bn|}的前20项之和
故答案为：D
点评：本题主要考查等差数列求和的前n项公式．考查学生的运算能力．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目