题目内容
已知双曲线(1)求此双曲线方程;
(2)求k,m的关系;
(3)求m的取值范围.
解:(1)过A(0,-b),B(a,0)的直线方程为bx-ay-ab=0.由距离公式得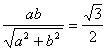 ,又e=
,又e=![]() ,
,
解得b=1,a=3.所以,双曲线方程为![]() -y2=1.
-y2=1.
(2)由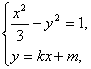 消去y,得(3k2-1)x2+6kmx+3(m2+1)=0①
消去y,得(3k2-1)x2+6kmx+3(m2+1)=0①
从题设知3k2-1≠0,Δ=(6km)2-12(3k2-1)(m2+1)>0
∴m2-3k2+1>0.②
设C(x1,y1),D(x2,y2),CD中点P(x3,y3),
∵C、D两点在以A为圆心的同一个圆上,∴P点为CD中点,且AP⊥CD.
从①式得x1+x2=![]() ,所以x3=
,所以x3=![]() .
.
由P(x3,y3)在直线y=kx+m上,得y3=kx3+m=![]() .
.
所以kAP=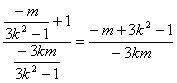 ,
,
由于AP⊥CD,故![]() =-1,
=-1,
化简得3k2=4m+1,③
综上得k、m间的关系:3k2=4m+1,且m2-3k2+1>0.
(3)由3k2=4m+1>0(k≠0),得m>![]() .
.
由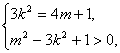 消去k,得m2-(4m+1)+1>0,
消去k,得m2-(4m+1)+1>0,
即m2-4m>0.解得m<0,或m>4.
所以![]() <m<0,或m>4.
<m<0,或m>4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目