题目内容
已知n次多项式Pn(x)=axn+a1xn-1+…+an-1x+an.如果在一种算法中,计算xk(k=2,3,4,…,n)的值需要k-1次乘法,计算P3(x)的值共需要9次运算(6次乘法,3次加法),那么计算Pn(x)的值共需要 次运算.
下面给出一种减少运算次数的算法:P(x)=a.Pn+1(x)=xPn(x)+ak+1(k=0,l,2,…,n-1).利用该算法,计算P3(x)的值共需要6次运算,计算Pn(x)的值共需要 次运算.
【答案】分析:本题考查的知识点是算法案例中的秦九韶算法,根据常规运算的算法规则,和秦九韶算法的算法规则,我们不难得到结论.
解答:解:在利用常规算法计算多项式Pn(x)=axn+a1xn-1+…+an-1x+an的值时,
算axn项需要n乘法,则在计算时共需要乘法:n+(n-1)+(n-2)+…+2+1=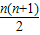 次
次
需要加法:n次,则计算Pn(x)的值共需要 n(n+3)次运算.
n(n+3)次运算.
在使用秦九韶算法计算多项式Pn(x)=axn+a1xn-1+…+an-1x+an的值时,
共需要乘法:n次
需要加法:n次,则计算Pn(x)的值共需要2n算.
故答案为: n(n+3),2n
n(n+3),2n
点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.
解答:解:在利用常规算法计算多项式Pn(x)=axn+a1xn-1+…+an-1x+an的值时,
算axn项需要n乘法,则在计算时共需要乘法:n+(n-1)+(n-2)+…+2+1=
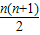 次
次需要加法:n次,则计算Pn(x)的值共需要
 n(n+3)次运算.
n(n+3)次运算.在使用秦九韶算法计算多项式Pn(x)=axn+a1xn-1+…+an-1x+an的值时,
共需要乘法:n次
需要加法:n次,则计算Pn(x)的值共需要2n算.
故答案为:
 n(n+3),2n
n(n+3),2n点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.

练习册系列答案
相关题目