题目内容
已知数列{an}满足an=2an-1+2n-1(n≥2)，且a1=5．(Ⅰ)若存在一个实数λ，使得数列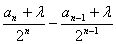
为等差数列，请求出λ的值；
(Ⅱ)在(Ⅰ)的条件下，求出数列an的前n项和Sn.
答案：解：(Ⅰ)假设存在实数λ符合题意，则必为与n无关的常数．
要使
是与n无关的常数，
则
=0，得λ=-1．
故存在实数λ=-1，使得数列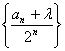
为等差数列．
(Ⅱ)由(Ⅰ)可得
=1，
∴d=1，且首项为
=2．
∴
=2+(n-1)=n+1，
∴an=(n+1)2n+1(n∈N+)
令bn=(n+1)2n且其前n项和为Tn，
∴Tn=2×2+3×22+4×23+…+(n+1)2n ①
2Tn=2×22+3×23+…+n×2n+(n+1)2n+1 ②
①-②得
-Tn=4+22+23+…+2n-(n+1)2n+1
=2+(2+…+2n)-(n+1)2n+1
=2n+1-(n+1)2n+1=-n·2n+1
∴Tn=n·2n+1，∴Sn=n·2n+1+n．
练习册系列答案
相关题目