题目内容
已知f(x)是定义在R上的函数,f(1)=1,且 x1,x2∈R,总有f(x1+x2)=f(x1)+f(x2)+1恒成立.
x1,x2∈R,总有f(x1+x2)=f(x1)+f(x2)+1恒成立.
(Ⅰ)求证:f(x)+1是奇函数;
(Ⅱ)对 n∈N*,有
n∈N*,有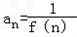 ,
,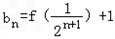 ,求:Sn=a1a2+a2a3+…+anan+1及
,求:Sn=a1a2+a2a3+…+anan+1及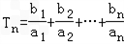 ;
;
(Ⅲ)求F(n)=an+1+an+2+…+a2n(n≥2,n∈N)的最小值.
 x1,x2∈R,总有f(x1+x2)=f(x1)+f(x2)+1恒成立.
x1,x2∈R,总有f(x1+x2)=f(x1)+f(x2)+1恒成立.(Ⅰ)求证:f(x)+1是奇函数;
(Ⅱ)对
 n∈N*,有
n∈N*,有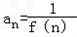 ,
,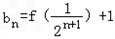 ,求:Sn=a1a2+a2a3+…+anan+1及
,求:Sn=a1a2+a2a3+…+anan+1及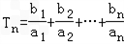 ;
;(Ⅲ)求F(n)=an+1+an+2+…+a2n(n≥2,n∈N)的最小值.
解:(1)证明:f(x1+x2)=f(x1)+f(x2)+1,
令x1=x2=0得f(0)=﹣1,
再令x1=x,x2=﹣x,得f(0)=f(x)+f(﹣x)+1
∴f(﹣x)+1=﹣[f(x)+1],函数f(x)+1是奇函数.
(2)令x1=n,x2=1得f(n+1)=f(n)+2,
所以f(n)=2n﹣1,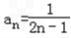 ,
,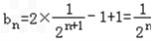 ,
,
∴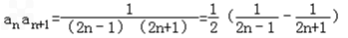
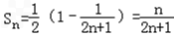
又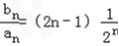 ,
,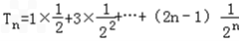 ①
①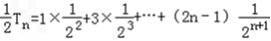 ②
②
由①﹣②得出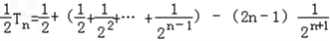
=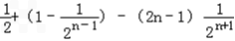
计算整理得出得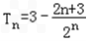 (3)∵
(3)∵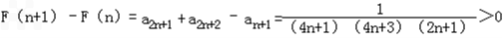
∴F(n+1)>F(n).
又n≥2,
∴F(n)的最小值为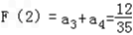
令x1=x2=0得f(0)=﹣1,
再令x1=x,x2=﹣x,得f(0)=f(x)+f(﹣x)+1
∴f(﹣x)+1=﹣[f(x)+1],函数f(x)+1是奇函数.
(2)令x1=n,x2=1得f(n+1)=f(n)+2,
所以f(n)=2n﹣1,
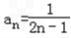 ,
,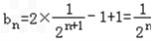 ,
,∴
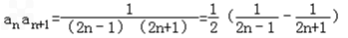
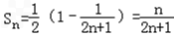
又
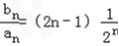 ,
,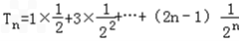 ①
①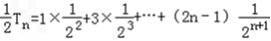 ②
②由①﹣②得出
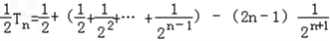
=
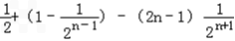
计算整理得出得
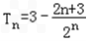 (3)∵
(3)∵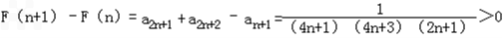
∴F(n+1)>F(n).
又n≥2,
∴F(n)的最小值为
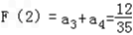

练习册系列答案
相关题目