题目内容
定义在R上的函数
是减函数，且函数
的图象关于（1，0）成中心对称，若实数
满足不等式
+
，则的取值范围是___________．
(-
,1]∪[2，
）
解析试题分析：因为函数的图象关于（1，0）成中心对称，所以函数的图象关于坐标原点对称，所以函数是奇函数，且是R上的减函数，所以由+可得
，所以
，所以的取值范围是(-,1]∪[2，）.
考点：本小题主要考查利用函数的性质解抽象不等式，考查学生的转化问题的能力和运算求解能力.
点评：解决本小题的关键是准确转化问题条件，灵活运算函数的性质.
练习册系列答案
相关题目
有一个正根和一个负根，则实数
的取值范围是_________________.
表示a，b两数中的最小值。若函数
的图像关于直线x=
对称，则t的值为 .
的定义域是 
，则
= 。
, 则使
为奇函数且在
上单调递增的
值的个数为 .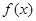 
在R上单调递减，则f(-1) f(3)(用＜、﹦、＞填空）
恰有两个不同的零点,则实数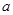
的取值范围是