题目内容
设a是实数,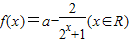 ,
,(1)试证明:对于任意a,f(x)在R为增函数;
(2)试确定a的值,使f(x)为奇函数.
【答案】分析:(1)设x1、x2∈R且x1<x2,用作差法,有f(x1)-f(x2)=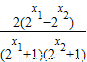 ,结合指数函数的单调性分析可得f(x1)-f(x2)<0,可得f(x)的单调性且与a的值无关;
,结合指数函数的单调性分析可得f(x1)-f(x2)<0,可得f(x)的单调性且与a的值无关;
(2)根据题意,假设f(x)是奇函数,由奇函数的定义可得,f(-x)=-f(x),即a-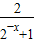 =-(a-
=-(a-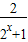 ),对其变形,解可得a的值,即可得答案.
),对其变形,解可得a的值,即可得答案.
解答:解:(1)证明:设x1、x2∈R且x1<x2,
f(x1)-f(x2)=(a-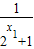 )-(a-
)-(a-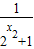 )=
)=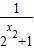 -
-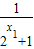 =
=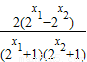 ,
,
又由y=2x在R上为增函数,则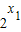 >0,
>0,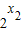 >0,
>0,
由x1<x2,可得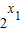 -
-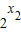 <0,
<0,
则f(x1)-f(x2)<0,
故f(x)为增函数,与a的值无关,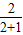
即对于任意a,f(x)在R为增函数;
(2)若f(x)为奇函数,且其定义域为R,
必有有f(-x)=-f(x),
即a-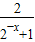 =-(a-
=-(a-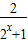 ),变形可得2a=
),变形可得2a=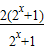 =2,
=2,
解可得,a=1,
即当a=1时,f(x)为奇函数.
点评:本题考查函数奇偶性、单调性的判断与应用,注意(1)中要体现f(x)的单调性与a的值无关.
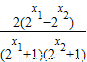 ,结合指数函数的单调性分析可得f(x1)-f(x2)<0,可得f(x)的单调性且与a的值无关;
,结合指数函数的单调性分析可得f(x1)-f(x2)<0,可得f(x)的单调性且与a的值无关;(2)根据题意,假设f(x)是奇函数,由奇函数的定义可得,f(-x)=-f(x),即a-
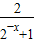 =-(a-
=-(a-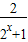 ),对其变形,解可得a的值,即可得答案.
),对其变形,解可得a的值,即可得答案.解答:解:(1)证明:设x1、x2∈R且x1<x2,
f(x1)-f(x2)=(a-
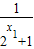 )-(a-
)-(a-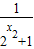 )=
)=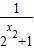 -
-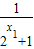 =
=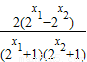 ,
,又由y=2x在R上为增函数,则
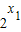 >0,
>0,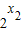 >0,
>0,由x1<x2,可得
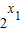 -
-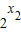 <0,
<0,则f(x1)-f(x2)<0,
故f(x)为增函数,与a的值无关,
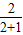
即对于任意a,f(x)在R为增函数;
(2)若f(x)为奇函数,且其定义域为R,
必有有f(-x)=-f(x),
即a-
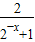 =-(a-
=-(a-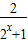 ),变形可得2a=
),变形可得2a=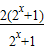 =2,
=2,解可得,a=1,
即当a=1时,f(x)为奇函数.
点评:本题考查函数奇偶性、单调性的判断与应用,注意(1)中要体现f(x)的单调性与a的值无关.

练习册系列答案
相关题目
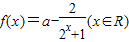 ,
,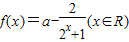 .
.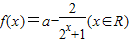 .
.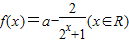 .
.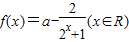 .
.