题目内容
已知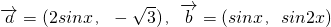 ,
,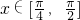 .
.
(1)若 ,求x的值;
,求x的值;
(2)若 ,求f(x)的最大值,并且求使f(x)取得最大值的x值;
,求f(x)的最大值,并且求使f(x)取得最大值的x值;
(3)令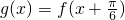 ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.
解:(1)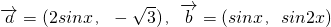 ,
, 所以
所以 =0,
=0, ,
,
2sin2x- sin2x=0即cos2x+
sin2x=0即cos2x+ sin2x=0,tan2x=
sin2x=0,tan2x= ,
,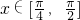 ,所以x=
,所以x= ;
;
(2)由(1)可知: =cos2x+
=cos2x+ sin2x=2sin(2x+
sin2x=2sin(2x+ ),所以函数的最大值为:2,此时2x+
),所以函数的最大值为:2,此时2x+ =
= +2kπ,k∈Z;
+2kπ,k∈Z;
所以x=kπ ,k∈Z;
,k∈Z;
(3)因为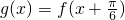 =2sin(2x+
=2sin(2x+ +
+ )=2cos2x,
)=2cos2x,
因为g(-x)=2cos(-2x)=2cos2x=g(x),所以函数是偶函数.
分析:(1)通过 ,得到数量积为0,化简函数表达式,即可求x的值;
,得到数量积为0,化简函数表达式,即可求x的值;
(2)通过数量积求出函数的表达式,然后化简为一个角的一个三角函数的形式,然后求f(x)的最大值及使f(x)取得最大值的x值;
(3)通过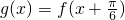 ,求出函数的表达式,利用奇偶性的定义直接判断函数g(x)的奇偶性,即可.
,求出函数的表达式,利用奇偶性的定义直接判断函数g(x)的奇偶性,即可.
点评:本题是中档题,通过向量的数量积,考查函数的基本性质,最大值,奇偶性的判断,函数值的求法,考查计算能力,常考题型.
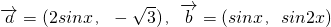 ,
, 所以
所以 =0,
=0, ,
,2sin2x-
 sin2x=0即cos2x+
sin2x=0即cos2x+ sin2x=0,tan2x=
sin2x=0,tan2x= ,
,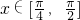 ,所以x=
,所以x= ;
;(2)由(1)可知:
 =cos2x+
=cos2x+ sin2x=2sin(2x+
sin2x=2sin(2x+ ),所以函数的最大值为:2,此时2x+
),所以函数的最大值为:2,此时2x+ =
= +2kπ,k∈Z;
+2kπ,k∈Z;所以x=kπ
 ,k∈Z;
,k∈Z;(3)因为
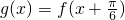 =2sin(2x+
=2sin(2x+ +
+ )=2cos2x,
)=2cos2x,因为g(-x)=2cos(-2x)=2cos2x=g(x),所以函数是偶函数.
分析:(1)通过
 ,得到数量积为0,化简函数表达式,即可求x的值;
,得到数量积为0,化简函数表达式,即可求x的值;(2)通过数量积求出函数的表达式,然后化简为一个角的一个三角函数的形式,然后求f(x)的最大值及使f(x)取得最大值的x值;
(3)通过
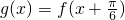 ,求出函数的表达式,利用奇偶性的定义直接判断函数g(x)的奇偶性,即可.
,求出函数的表达式,利用奇偶性的定义直接判断函数g(x)的奇偶性,即可.点评:本题是中档题,通过向量的数量积,考查函数的基本性质,最大值,奇偶性的判断,函数值的求法,考查计算能力,常考题型.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 ,
,
 ,求实数
,求实数 的值;
的值; ,求实数
,求实数 。
。 ,求
,求 及
及 ;
; ,求
,求 。
。
 .
. ,求函数
,求函数 的单调递减区间;
的单调递减区间; 是函数
是函数 ,求实数
,求实数 的取值范围.
的取值范围. ,
, ,求函数
,求函数 的最大值与最小值;
的最大值与最小值; ,且
,且 ,求
,求