题目内容
已知椭圆C: 的右焦点为F,离心率
的右焦点为F,离心率 ,椭圆C上的点到F的距离的最大值为
,椭圆C上的点到F的距离的最大值为 ,直线l过点F与椭圆C交于不同的两点A、B.
,直线l过点F与椭圆C交于不同的两点A、B.(1)求椭圆C的方程;
(2)若
 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(1)由题意心率 ,椭圆C上的点到右焦点F的距离的最大值为
,椭圆C上的点到右焦点F的距离的最大值为 ,可以建立关于a,b,c的方程解出即可;
,可以建立关于a,b,c的方程解出即可;
(2)由题意分设出直线的方程把直线方程与椭圆方程进行联立,利用根与系数的关系及弦长公式求解即可建立方程求得.
解答:解:(1)由题意知, ,
,
所以 ,从而b=1,
,从而b=1,
故椭圆C的方程为
(2)容易验证直线l的斜率不为0,故可设直线l的方程为x=my+1,代入 中,
中,
得(m2+2)y2+2my-1=0.
设A(x1,y1),B(x2,y2)
则由根与系数的关系,得
 ,
,
 =
= ,
,
解得m=± ,
,
所以直线l的方程为 ,即
,即 或
或 .
.
点评:此题考查了椭圆的标准方程及其基本性质,求解时用到了方程的思想,还考查了直线方程与椭圆方程联立后利用根与系数的关系设而不求整体代换的思想,还考查了弦长公式.
 ,椭圆C上的点到右焦点F的距离的最大值为
,椭圆C上的点到右焦点F的距离的最大值为 ,可以建立关于a,b,c的方程解出即可;
,可以建立关于a,b,c的方程解出即可;(2)由题意分设出直线的方程把直线方程与椭圆方程进行联立,利用根与系数的关系及弦长公式求解即可建立方程求得.
解答:解:(1)由题意知,
 ,
,所以
 ,从而b=1,
,从而b=1,故椭圆C的方程为

(2)容易验证直线l的斜率不为0,故可设直线l的方程为x=my+1,代入
 中,
中,得(m2+2)y2+2my-1=0.
设A(x1,y1),B(x2,y2)
则由根与系数的关系,得

 ,
, =
= ,
,解得m=±
 ,
,所以直线l的方程为
 ,即
,即 或
或 .
.点评:此题考查了椭圆的标准方程及其基本性质,求解时用到了方程的思想,还考查了直线方程与椭圆方程联立后利用根与系数的关系设而不求整体代换的思想,还考查了弦长公式.

练习册系列答案
相关题目
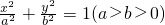 的右焦点为F(1,0),左、右顶点分别A、B,其中B点的坐标为(2,0).
的右焦点为F(1,0),左、右顶点分别A、B,其中B点的坐标为(2,0). 的取值范围.
的取值范围.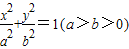 的右焦点为F,离心率
的右焦点为F,离心率 ,椭圆C上的点到F的距离的最大值为
,椭圆C上的点到F的距离的最大值为 ,直线l过点F与椭圆C交于不同的两点A、B.
,直线l过点F与椭圆C交于不同的两点A、B. ,求直线l的方程.
,求直线l的方程. 的右焦点为F,离心率
的右焦点为F,离心率 ,椭圆C上的点到F的距离的最大值为
,椭圆C上的点到F的距离的最大值为 ,直线l过点F与椭圆C交于不同的两点A、B.
,直线l过点F与椭圆C交于不同的两点A、B. ,求直线l的方程.
,求直线l的方程. 的右焦点为F,离心率
的右焦点为F,离心率 ,椭圆C上的点到F的距离的最大值为
,椭圆C上的点到F的距离的最大值为 ,直线l过点F与椭圆C交于不同的两点A、B.
,直线l过点F与椭圆C交于不同的两点A、B. ,求直线l的方程.
,求直线l的方程.