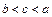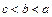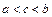题目内容
(本题满分12分)
设函数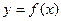
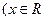 且
且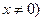 对任意非零实数
对任意非零实数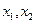 恒有
恒有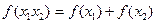 ,且对任意
,且对任意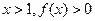 .
.
(Ⅰ)求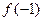 及
及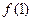 的值;
的值;
(Ⅱ)判断函数 的奇偶性;
的奇偶性;
(Ⅲ)求方程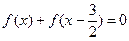 的解.
的解.
设函数
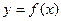
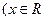 且
且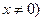 对任意非零实数
对任意非零实数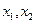 恒有
恒有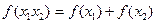 ,且对任意
,且对任意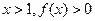 .
. (Ⅰ)求
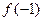 及
及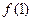 的值;
的值; (Ⅱ)判断函数
 的奇偶性;
的奇偶性;(Ⅲ)求方程
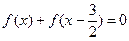 的解.
的解.(Ⅰ)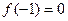 ,
,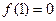
(Ⅱ)函数 是偶函数.
是偶函数.
(Ⅲ)方程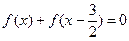 的解集为
的解集为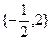 .
.
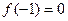 ,
,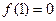
(Ⅱ)函数
 是偶函数.
是偶函数.(Ⅲ)方程
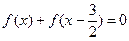 的解集为
的解集为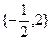 .
.解:(Ⅰ)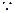 对任意非零实数
对任意非零实数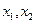 恒有
恒有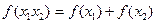 ,
,
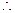 令
令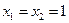 代入可得
代入可得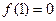 ,┈┈ 1分
,┈┈ 1分
又令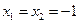 ,代入并利用
,代入并利用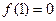 ,可得
,可得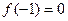 .┈┈ 1分
.┈┈ 1分
(Ⅱ)取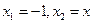 ,代入得
,代入得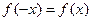 ,又函数定义域为
,又函数定义域为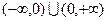 ,
,
 函数
函数 是偶函数. ┈┈ 2分
是偶函数. ┈┈ 2分
(Ⅲ)函数 在
在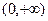 上为单调递增函数,证明如下:
上为单调递增函数,证明如下:
任取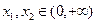 且
且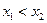 ,则
,则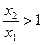 ,由题设有
,由题设有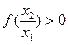 ,
,
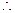
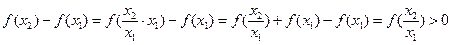 ,
,
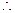
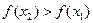 ,即函数
,即函数 在
在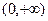 上为单调递增函数;┈┈ 4分
上为单调递增函数;┈┈ 4分
由(Ⅱ)函数 是偶函数,
是偶函数,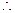 函数
函数 在
在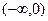 上为单调递减函数;┈┈ 1分
上为单调递减函数;┈┈ 1分
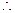
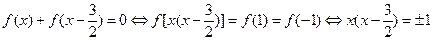
解得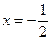 或
或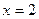 ,┈┈ 2分
,┈┈ 2分
 方程
方程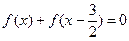 的解集为
的解集为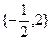 .┈┈ 1分
.┈┈ 1分
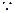 对任意非零实数
对任意非零实数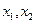 恒有
恒有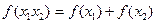 ,
,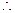 令
令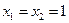 代入可得
代入可得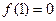 ,┈┈ 1分
,┈┈ 1分又令
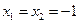 ,代入并利用
,代入并利用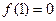 ,可得
,可得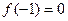 .┈┈ 1分
.┈┈ 1分(Ⅱ)取
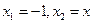 ,代入得
,代入得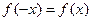 ,又函数定义域为
,又函数定义域为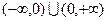 ,
,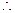 函数
函数 是偶函数. ┈┈ 2分
是偶函数. ┈┈ 2分(Ⅲ)函数
 在
在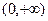 上为单调递增函数,证明如下:
上为单调递增函数,证明如下:任取
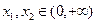 且
且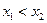 ,则
,则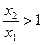 ,由题设有
,由题设有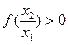 ,
,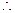
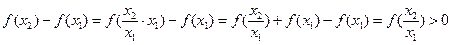 ,
,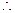
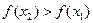 ,即函数
,即函数 在
在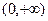 上为单调递增函数;┈┈ 4分
上为单调递增函数;┈┈ 4分由(Ⅱ)函数
 是偶函数,
是偶函数,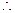 函数
函数 在
在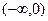 上为单调递减函数;┈┈ 1分
上为单调递减函数;┈┈ 1分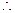
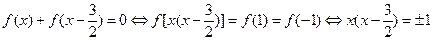
解得
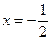 或
或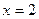 ,┈┈ 2分
,┈┈ 2分 方程
方程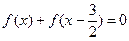 的解集为
的解集为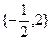 .┈┈ 1分
.┈┈ 1分
练习册系列答案
相关题目
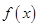 是奇函数,当
是奇函数,当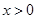 时,
时,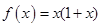 ;当
;当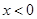 时,
时,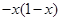
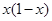

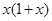
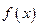 的定义域为
的定义域为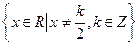 ,且
,且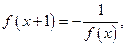 如果
如果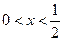 时,
时,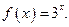
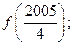
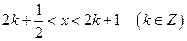 时,求
时,求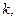 使得当
使得当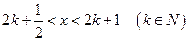 时,
时,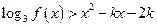 有实数解.
有实数解.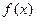 既是奇函数,又是周期为3的周期函数,当
既是奇函数,又是周期为3的周期函数,当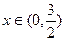 时,
时,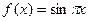 ,
,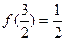 ,则函数
,则函数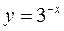
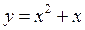
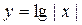
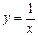
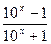
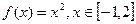
 的是 ( )
的是 ( ) 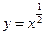
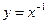
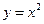
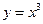
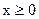 时,
时,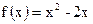 , 则
, 则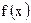 在
在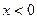 时的解析式是 _______________
时的解析式是 _______________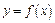 是偶函数,而
是偶函数,而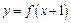 是奇函数,且对任意
是奇函数,且对任意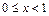 ,都有
,都有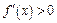 ,则
,则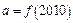 ,
,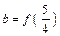 ,
,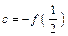 的大小关系是
的大小关系是