Question

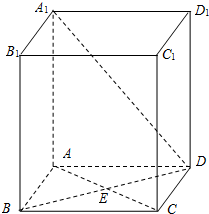（2006•静安区二模）如图所示，已知正四面体ABCD的棱长为2，点E为棱AD的中点，求：
（1）正四面体ABCD的体积；
（2）直线CE与平面BCD所成的角的大小（用反三角函数值表示）．

Answer 1

分析：（1）根据棱长为a的正四面体高为

6

3

a，底面面积为

3

4

a2，体积为

2

12

a3，将a=2，代入棱锥体积公式，可得答案．
（2）过点E作EF⊥面BCD于F，∠ECF就是所求的角，解Rt△ECF可得答案．

解答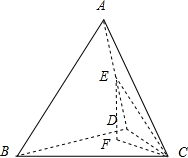：解：（1）棱长为2的正四面体
高h=

2 6

3

…（2分），
底面积S=

3

…（2分），
体积V=

2 2

3

…（6分）
（说明：直接由公式计算得出正确结果不扣分）
（2）过点E作EF⊥面BCD于F，∠ECF就是所求的角，…（8分）
在Rt△ECF中，EF=

1

2

h=

6

3

，CE=

3

，
∴sin∠ECF=

EF

CE

=

2

3

，…（10分）
所以CE与平面BCD所成角为arcsin

2

3

（12分）

点评：本题考查的知识点是直线与平面所成的角，棱锥体积公式，解答（1）的关键是熟练掌握与正四面体相关的公式，（2）的关键是构造出线在夹角的平面角