题目内容
已知二次函数f(x)满足f(-1)=0,且x≤f(x)≤ (x2+1)对一切实数x恒成立.
(x2+1)对一切实数x恒成立.
(1)求f(1);
(2)求f(x)的解析表达式.
解:(1)∵二次函数f(x)满足f(-1)=0,
且x≤f(x)≤ (x2+1)对一切实数x恒成立,
(x2+1)对一切实数x恒成立,
∴取x=1,得1≤f(1)≤ (1+1),
(1+1),
所以f(1)=1.
(2)设f(x)=ax2+bx+c(a≠0)
因f(-1)=0,f(1)=1,
∴ ,
,
∴a+c=b= ,
,
∵f(x)≥x对x∈R恒成立,
∴ax2+(b-1)x+c≥0对x∈R恒成立,
∴
∴
∵a>0,ac≥ >0,
>0,
∴c>0.
∵ =a+c≥2
=a+c≥2 ≥2
≥2 当且仅当a=c=
当且仅当a=c= 时,等式成立,
时,等式成立,
∴f(x)=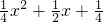 .
.
分析:(1)取x=1,由1≤f(1)≤ (1+1),能够求出f(1)的值.
(1+1),能够求出f(1)的值.
(2)设f(x)=ax2+bx+c(a≠0),由f(-1)=0,f(1)=1,知 ,所以a+c=b=
,所以a+c=b= ,由f(x)≥x,对x∈R恒成立,知ax2+(b-1)x+c≥0对x∈R恒成立,由此能求出f(x)的表达式.
,由f(x)≥x,对x∈R恒成立,知ax2+(b-1)x+c≥0对x∈R恒成立,由此能求出f(x)的表达式.
点评:本题考查二次函数的性质的综合应用,考查函数解析式的求法,解题时要认真审题,仔细解答,注意函数恒成立条件的灵活运用.
且x≤f(x)≤
 (x2+1)对一切实数x恒成立,
(x2+1)对一切实数x恒成立,∴取x=1,得1≤f(1)≤
 (1+1),
(1+1),所以f(1)=1.
(2)设f(x)=ax2+bx+c(a≠0)
因f(-1)=0,f(1)=1,
∴
 ,
,∴a+c=b=
 ,
,∵f(x)≥x对x∈R恒成立,
∴ax2+(b-1)x+c≥0对x∈R恒成立,
∴

∴

∵a>0,ac≥
 >0,
>0,∴c>0.
∵
 =a+c≥2
=a+c≥2 ≥2
≥2 当且仅当a=c=
当且仅当a=c= 时,等式成立,
时,等式成立,∴f(x)=
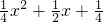 .
.分析:(1)取x=1,由1≤f(1)≤
 (1+1),能够求出f(1)的值.
(1+1),能够求出f(1)的值.(2)设f(x)=ax2+bx+c(a≠0),由f(-1)=0,f(1)=1,知
 ,所以a+c=b=
,所以a+c=b= ,由f(x)≥x,对x∈R恒成立,知ax2+(b-1)x+c≥0对x∈R恒成立,由此能求出f(x)的表达式.
,由f(x)≥x,对x∈R恒成立,知ax2+(b-1)x+c≥0对x∈R恒成立,由此能求出f(x)的表达式.点评:本题考查二次函数的性质的综合应用,考查函数解析式的求法,解题时要认真审题,仔细解答,注意函数恒成立条件的灵活运用.

练习册系列答案
相关题目