Question

【题目】设向量， ，记

(1)求函数f(x)的最小正周期；

(2)试用“五点法”画出函数f(x)在区间上的简图，并指出该函数的图象可由y＝sin x(x∈R)的图象经过怎样的平移和伸缩变换得到；

(3)若函数g(x)＝f(x)＋m， 的最小值为2，试求出函数g(x)的最大值．

Answer 1

【答案】（1）；（2）见解析；（3）

【解析】试题分析：(1)利用平面向量的数量积公式、配角公式进行化简，再利用周期公式进行求解；(2)利用整体思想和“五点作图法”进行求解，再利用图象变换得到变化过程；（3）利用三角函数的单调性进行求解．

试题解析：(1)f(x)＝a·b＝sin xcos x＋cos2x＝sin 2x＋

＝sin(2x＋)＋，

∴函数f(x)的最小正周期T＝＝π.

(2)列表如下：

x	－
2x＋	0		π		2π
sin(2x＋)	0	1	0	－1	0
y				－

描点，连线得函数f(x)在区间上的简图如图所示：

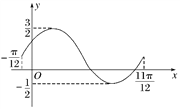
y＝sin x的图象向左平移个单位长度后得到y＝sin(x＋)的图象，再保持纵坐标不变，横坐标缩短为原来的后得到y＝sin(2x＋)的图象，最后将y＝sin(2x＋)的图象向上平移个单位长度后得到y＝sin(2x＋)＋的图象．

(3)g(x)＝f(x)＋m＝sin(2x＋)＋＋m.

∵x∈，∴2x＋∈，∴sin(2x＋)∈，

∴g(x)的值域为.

又函数g(x)的最小值为2，∴m＝2，∴g(x)max＝＋m＝.