题目内容
16. 三棱柱A的直观图(图1)及三视图(图2)(主视图和俯视图是正方形,左视图是等腰直角三角形)如图所示,A为A的中点.
三棱柱A的直观图(图1)及三视图(图2)(主视图和俯视图是正方形,左视图是等腰直角三角形)如图所示,A为A的中点.(Ⅰ)求证:B1C⊥平面BAC1;
(Ⅱ)求平面C1BA与平面C1BD的夹角的余弦值.
分析 (Ⅰ)先证明AB⊥平面C1B1BC,可得AB⊥B1C,利用BC1⊥B1C,即可证明:B1C⊥平面BAC1;
(Ⅱ)补成正方体,得∠O1OS为二面角的平面角,即可求平面C1BA与平面C1BD的夹角的余弦值
解答 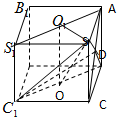 解:(Ⅰ)由三视图可知,几何体为直三棱柱.
解:(Ⅰ)由三视图可知,几何体为直三棱柱.
∵AB⊥BC,BB1⊥AB,BC∩BB1=B,
∴AB⊥平面C1B1BC,∴AB⊥B1C,…(4分)
在正方形BB1C1C中,BC1⊥B1C,…(5分)
又∵BC1?平面ABC1,AB?平面ABC1,BC1∩AB=B,
∴B1C⊥平面ABC1.…(6分)
(Ⅱ)如图补成正方体,得∠O1OS为二面角的平面角,${O_1}O=2,{O_1}S=\sqrt{2}$,
∴$cos∠{O_1}OS=\frac{{\sqrt{6}}}{3}$,
∴平面C1BA与平面C1BD的夹角的余弦值为$\frac{\sqrt{6}}{3}$.…(12分)
点评 本题考查线面垂直的判定与性质,考查面面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.两条直线都与一个平面平行,则这两条直线的位置关系是( )
| A. | 异面 | B. | 相交 | ||
| C. | 可能共面,也可能异面 | D. | 平行 |
