题目内容
已知函数
（k∈R），若函数y=|f（x）|+k有三个零点，则实数k的取值范围是（ ）A．k≤2
B．-1＜k＜0
C．-2≤k＜-1
D．k≤-2
【答案】分析：由题意可得|f（x）|=-k≥0，进而可得k≤0，作出图象，结合图象可得答案．
解答：
解：由y=|f（x）|+k=0得|f（x）|=-k≥0，所以k≤0，作出函数y=|f（x）|的图象，
由图象可知：要使y=-k与函数y=|f（x）|有三个交点，
则有-k≥2，即k≤-2，
故选D．
点评：本题考查根的存在性及个数的判断，作出函数的图象是解决问题的关键，属中档题．
解答：
解：由y=|f（x）|+k=0得|f（x）|=-k≥0，所以k≤0，作出函数y=|f（x）|的图象，由图象可知：要使y=-k与函数y=|f（x）|有三个交点，
则有-k≥2，即k≤-2，
故选D．
点评：本题考查根的存在性及个数的判断，作出函数的图象是解决问题的关键，属中档题．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
（k∈R），若函数
有三个零点，则实数k的取值范围是（ ）
（k∈R）．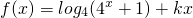
（k∈R）是偶函数．
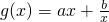（a、b是正常数）在区间
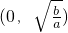上为减函数，在区间
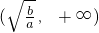上为增函数．参考该定理，解决下面问题：是否存在实数m同时满足以下两个条件：①不等式
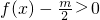恒成立；②方程f（x）-m=0有解．若存在，试求出实数m的取值范围，若不存在，请说明理由．
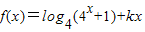（k∈R）是偶函数．
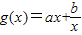（a、b是正常数）在区间
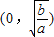上为减函数，在区间
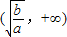上为增函数．参考该定理，解决下面问题：是否存在实数m同时满足以下两个条件：①不等式
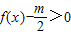恒成立；②方程f（x）-m=0有解．若存在，试求出实数m的取值范围，若不存在，请说明理由．
（k∈R）．
，若函数f（x）与g（x）的图象有且只有一个公共点，求实数a的取值范围．