题目内容
若点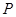 在直线
在直线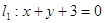 上,过点
上,过点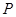 的直线
的直线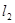 与曲线
与曲线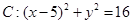 只有一个公共点
只有一个公共点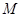 ,则
,则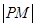 的最小值为__________。
的最小值为__________。
【答案】
4
【解析】
试题分析:因为(x-5)2+y2=16的圆心(5,0),半径为4,则圆心到直线的距离为:
 ,点P在直线l1:x+y+3=0上,过点P的直线l2与曲线C:(x-5)2+y2=16只有一个公共点M,则|PM|的最小值:
,点P在直线l1:x+y+3=0上,过点P的直线l2与曲线C:(x-5)2+y2=16只有一个公共点M,则|PM|的最小值: ,故答案为:4
,故答案为:4
考点:本题是基础题,考查点到直线的距离公式,直线与圆的位置关系,勾股定理的应用,考查计算能力,转化思想的应用
点评:解决该试题的关键是求出圆心坐标,圆的半径,结合题意,利用圆的到直线的距离,半径,|PM|满足勾股定理,求出|PM|就是最小值.

练习册系列答案
相关题目
 在直线
在直线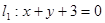 上,过点
上,过点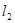 与曲线
与曲线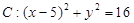 只有一个公共点
只有一个公共点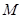 ,则
,则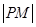 的最小值为__________。
的最小值为__________。 在直线
在直线 上,过点
上,过点 与曲线
与曲线 只有一个公共点
只有一个公共点 ,则
,则 的最小值为__________.
的最小值为__________. 在直线
在直线 上,过点
上,过点 与曲线
与曲线 只有一个公共点
只有一个公共点 ,则
,则 的最小值为__________
的最小值为__________