题目内容
已知函数f(x)=ax3-bx2+9x+2,若f(x)在x=1处的切线方程为3x+y-6=0,
(Ⅰ)求f(x)的解析式及单调区间;
(Ⅱ)若对任意的x∈[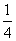 ,2]都有f(x)≥t2-2t-1成立,求函数g(t)=t2+t-2的最值。
,2]都有f(x)≥t2-2t-1成立,求函数g(t)=t2+t-2的最值。
(Ⅰ)求f(x)的解析式及单调区间;
(Ⅱ)若对任意的x∈[
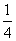 ,2]都有f(x)≥t2-2t-1成立,求函数g(t)=t2+t-2的最值。
,2]都有f(x)≥t2-2t-1成立,求函数g(t)=t2+t-2的最值。 解:由已知,得切点为(1,3),且f′(x)=3ax2-2bx+9,
(Ⅰ)由题意可得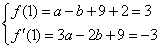 ,解得
,解得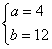 ,
,
故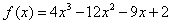 ,
,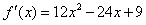 ,
,
由f′(x)=0,得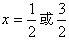 ,
,
由f′(x)>0,得 ;由f′(x)<0,得
;由f′(x)<0,得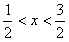 ;
;
f(x)的单调增区间为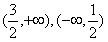 ,f(x)的单调减区间为
,f(x)的单调减区间为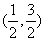 。
。
(Ⅱ)由(Ⅰ)可知f(x)的极小值为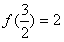 ,
,
又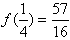 ,f(2)=4,
,f(2)=4,
∴f(x)在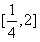 上的最小值为2,
上的最小值为2,
由f(x)≥t2-2t-1对x∈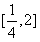 恒成立,则t2-2t-1≤2,
恒成立,则t2-2t-1≤2,
则t2-2t-3≤0,解得-1≤t≤3,
而g(t)=t2+t-2=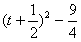 ,
,
故当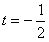 时,g(t)最小值为
时,g(t)最小值为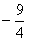 ;当t=3时,g(t)最大值为10。
;当t=3时,g(t)最大值为10。
(Ⅰ)由题意可得
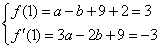 ,解得
,解得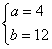 ,
,故
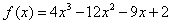 ,
,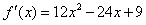 ,
,由f′(x)=0,得
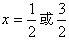 ,
,由f′(x)>0,得
 ;由f′(x)<0,得
;由f′(x)<0,得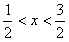 ;
;f(x)的单调增区间为
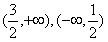 ,f(x)的单调减区间为
,f(x)的单调减区间为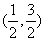 。
。(Ⅱ)由(Ⅰ)可知f(x)的极小值为
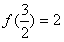 ,
,又
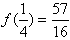 ,f(2)=4,
,f(2)=4,∴f(x)在
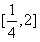 上的最小值为2,
上的最小值为2,由f(x)≥t2-2t-1对x∈
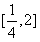 恒成立,则t2-2t-1≤2,
恒成立,则t2-2t-1≤2,则t2-2t-3≤0,解得-1≤t≤3,
而g(t)=t2+t-2=
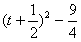 ,
,故当
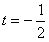 时,g(t)最小值为
时,g(t)最小值为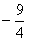 ;当t=3时,g(t)最大值为10。
;当t=3时,g(t)最大值为10。
练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |