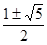题目内容

当x≠0时，函数y=3x+
1
2x
的值域为（　　）
分析：利用基本不等式，可求出x＞0时，函数值y的范围，结合函数为奇函数，可得x＜0时，函数值y的范围，综合讨论结果，可得答案
解答：解：当x＞0时，y=3x+
1
2x
≥2
3x•
1
2x
=
6

又由函数y=3x+
1
2x
为奇函数，
则当x＜0时，y=3x+
1
2x
≤-
6

综上所述，函数y=3x+
1
2x
的值域为(-∞，-
6
]∪[
6
，+∞)
故选B
点评：本题以求函数的值域为载体考查了基本不等式及函数奇偶性的性质，难度中档．
练习册系列答案
相关题目
设函数f（x）=x|x|+bx+c，给出下列四个命题（　　）
①当b≥0时，函数y=f（x）是单调函数；
②当b=0，c＞0时，方程f（x）=0只有一个实根；
③函数y=f（x）的图象关于点（0，c）对称；
④方程f（x）=0至多有3 个实根，其中正确命题的个数为．
A、1个B、2个C、3个D、4个
已知函数f（x）满足f（x）+f'（0）-e-x=-1，函数g（x）=-λlnf（x）+sinx是区间[-1，1]上的减函数．
（1）当x≥0时，曲线y=f（x）在点M（t，f（t））的切线与x轴、y轴围成的三角形面积为S（t），求S（t）的最大值；
（2）若g（x）＜t2+λt+1在x∈[-1，1]时恒成立，求t的取值范围；
（3）设函数h（x）=-lnf（x）-ln（x+m），常数m∈Z，且m＞1，试判定函数h（x）在区间[e-m-m，e2m-m]内的零点个数，并作出证明．

当x≠0时，函数y＝3x＋的值域是

[　　]
A．

[－，]

B．

(－∞，－]∪(，＋∞)

C．

(－∞，－]∪[，＋∞)

D．

[，＋∞)

 当x∈(0,+∞)时,幂函数y=(m2－m－1)为减函数, 则实数m的值为(   )

A. m=2    B. m=－1    C .m=－1或m=2    D .m≠

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网