题目内容
 已知函数f(x)=Asin(ωx+?)(A>0,ω>0,x∈R)在一个周期内的图象如图所示,则函数的解析式为________.
已知函数f(x)=Asin(ωx+?)(A>0,ω>0,x∈R)在一个周期内的图象如图所示,则函数的解析式为________.
f(x)=2sin( x+
x+ )
)
分析:由函数f(x)=Asin(ωx+?)的图象可知A=2,T=4π,从而可求ω,再由ω× +φ=
+φ= +2kπ可求得φ,从而可得答案.
+2kπ可求得φ,从而可得答案.
解答:∵f(x)=Asin(ωx+?)(A>0,ω>0,x∈R),
∴A=2,周期T= =
=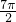 -(-
-(- )=4π,
)=4π,
∴ω= .
.
∴f(x)=2sin( x+?),
x+?),
又f(- )=2sin(
)=2sin( ×(-
×(- )+?)=0,f(
)+?)=0,f( )=2sin(
)=2sin( ×(
×( )+?)=2,
)+?)=2,
∴φ- =kπ,k∈Z,且φ+
=kπ,k∈Z,且φ+ =2kπ+
=2kπ+ ,k∈Z
,k∈Z
∴φ=2kπ+ .
.
∴f(x)=2sin( x+
x+ ).
).
故答案为:f(x)=2sin( x+
x+ ).
).
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,由ω× +φ=
+φ= +2kπ确定φ是难点,属于中档题.
+2kπ确定φ是难点,属于中档题.
 x+
x+ )
)分析:由函数f(x)=Asin(ωx+?)的图象可知A=2,T=4π,从而可求ω,再由ω×
 +φ=
+φ= +2kπ可求得φ,从而可得答案.
+2kπ可求得φ,从而可得答案.解答:∵f(x)=Asin(ωx+?)(A>0,ω>0,x∈R),
∴A=2,周期T=
 =
=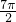 -(-
-(- )=4π,
)=4π,∴ω=
 .
.∴f(x)=2sin(
 x+?),
x+?),又f(-
 )=2sin(
)=2sin( ×(-
×(- )+?)=0,f(
)+?)=0,f( )=2sin(
)=2sin( ×(
×( )+?)=2,
)+?)=2,∴φ-
 =kπ,k∈Z,且φ+
=kπ,k∈Z,且φ+ =2kπ+
=2kπ+ ,k∈Z
,k∈Z∴φ=2kπ+
 .
.∴f(x)=2sin(
 x+
x+ ).
).故答案为:f(x)=2sin(
 x+
x+ ).
).点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,由ω×
 +φ=
+φ= +2kπ确定φ是难点,属于中档题.
+2kπ确定φ是难点,属于中档题. 
练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目