题目内容
【题目】已知函数f（x）=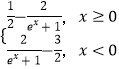 
（1）求函数f（x）的零点；
（2）若实数t满足f（log2t）+f（log2 
）＜2f（2），求f（t）的取值范围．
【答案】
（1）解：当x＜0时，解 
得：x=ln 
=﹣ln3，
当x≥0时，解 
得：x=ln3，
故函数f（x）的零点为±ln3；
（2）解：当x＞0时，﹣x＜0，
此时f（﹣x）﹣f（x）= 
= 
=0，
故函数f（x）为偶函数，
又∵x≥0时，f（x）= 
为增函数，
∴f（log2t）+f（log2 
）＜2f（2）时，2f（log2t）＜2f（2），
即|log2t|＜2，
﹣2＜log2t＜2，
∴t∈（ 
，4）
故f（t）∈（ 
， 
）
【解析】（1）分类讨论，函数对应方程根的个数，综合讨论结果，可得答案．（2）分析函数的奇偶性和单调性，进而可将不等式化为|log2t|＜2，解得f（t）的取值范围．
练习册系列答案
相关题目
