题目内容
已知函数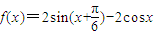 ,
,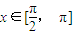 .
.(1)若
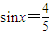 ,求函数f(x)的值;
,求函数f(x)的值;(2)求函数f(x)的值域.
【答案】分析:(1)先利用同角三角函数的基本关系求得cosx的值,代入到函数解析式,利用两角和公式展开后求得答案.
(2)利用两角和公式对函数解析式化简整理,然后利用x的范围和正弦函数的单调性求得函数的值域.
解答:解:(1)∵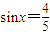 ,
,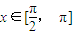
∴cosx=-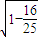 =-
=-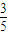
∴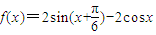 =
=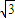 sinx+cosx-2cosx=
sinx+cosx-2cosx=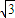 sinx-cosx=
sinx-cosx=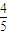 ×
×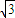 +
+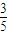 =
=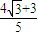
(2)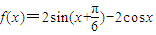 =
=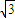 sinx+cosx-2cosx=
sinx+cosx-2cosx=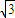 sinx-cosx=2sin(x-
sinx-cosx=2sin(x-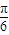 )
)
∵
∴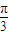 ≤x-
≤x-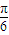 ≤
≤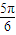
∴ ≤sin(x-
≤sin(x-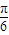 )≤1
)≤1
∴f(x)的最大值为2,最小值为1,值域为[1,2]
点评:本题主要考查了三角函数化简求值,两角和公式的化简,同角三角函数的基本关系的应用.解题时注意角的范围,判断三角函数的正负.
(2)利用两角和公式对函数解析式化简整理,然后利用x的范围和正弦函数的单调性求得函数的值域.
解答:解:(1)∵
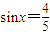 ,
,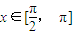
∴cosx=-
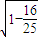 =-
=-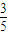
∴
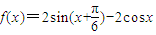 =
=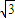 sinx+cosx-2cosx=
sinx+cosx-2cosx=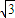 sinx-cosx=
sinx-cosx=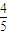 ×
×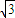 +
+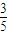 =
=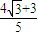
(2)
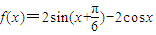 =
=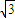 sinx+cosx-2cosx=
sinx+cosx-2cosx=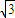 sinx-cosx=2sin(x-
sinx-cosx=2sin(x-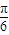 )
)∵

∴
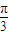 ≤x-
≤x-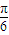 ≤
≤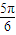
∴
 ≤sin(x-
≤sin(x-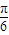 )≤1
)≤1∴f(x)的最大值为2,最小值为1,值域为[1,2]
点评:本题主要考查了三角函数化简求值,两角和公式的化简,同角三角函数的基本关系的应用.解题时注意角的范围,判断三角函数的正负.

练习册系列答案
相关题目
 ,
, .
. 且
且 ,试讨论
,试讨论 的单调性;
的单调性; ,总
,总 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.