题目内容
16．命题$p：?{x_0}∈R，{x_0}^2-2{x_0}-1＞0$，则命题?p：?x∈R，x2-2x-1≤0．分析 利用特称命题的否定是全称命题写出结果即可．
解答 解：∵特称命题的否定是全称命题．
∴命题p：?x0∈R，使x02-2x0-1＞0的否定是：?x∈R，x2-2x-1≤0．
故答案为：?x∈R，x2-2x-1≤0．
点评 本题考查命题的否定，注意量词的变化，基本知识的考查．
练习册系列答案
相关题目
1．
已知平行四边形ABCD中，点E为CD的中点，$\overrightarrow{AM}$=m•$\overrightarrow{AB}$，$\overrightarrow{AN}$=n$\overrightarrow{AD}$（m•n≠0），若$\overrightarrow{MN}$∥$\overrightarrow{BE}$，则$\frac{n}{m}$等于（ ）
已知平行四边形ABCD中，点E为CD的中点，$\overrightarrow{AM}$=m•$\overrightarrow{AB}$，$\overrightarrow{AN}$=n$\overrightarrow{AD}$（m•n≠0），若$\overrightarrow{MN}$∥$\overrightarrow{BE}$，则$\frac{n}{m}$等于（ ）| A． | 1 | B． | 2 | C． | $\frac{1}{2}$ | D． | -2 |
8．由直线x-y+1=0，x+y-5=0和x-1=0所围成的三角形区域（包括边界）用不等式组可表示为（ ）
| A． | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≥0}\\{x≤1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≤1}\end{array}\right.$ |
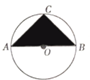如图，等腰直角△ABC内接于以AB为直径的圆O，假设你在圆形上随机撒一粒黄豆，则黄豆落到阴影部分的概率为$\frac{1}{π}$．