题目内容
函数f(x)=ax3+bx(a≠0)图象在点(1,f(1))处的切线与直线6x+y+7=0平行,导函数f′(x)的最小值为-12.
(1)求a、b的值;
(2)讨论方程f(x)=m解的情况(相同根算一根).
解:(1)∵f′(x)=3ax2+b的最小值为-12
∴b=-12,且a>0
又直线6x+y+7=0的斜率为-6
∵函数f(x)=ax3+bx(a≠0)图象在点(1,f(1))处的切线与直线6x+y+7=0平行
∴f'(1)=3a+b=-6
∴a=2
∴a=2,b=-12
(2)由(1)知f(x)=2x3-12x, ,列表如下:
,列表如下:
所以,函数f(x)的单调增区间是(-∞, )和
)和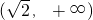
∴f(x)在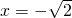 时取得极大值为
时取得极大值为 ,f(x)在
,f(x)在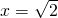 时取得极小值为
时取得极小值为
∴当 或
或 时,方程有一根;
时,方程有一根;
当 或
或 时,方程有两个根;
时,方程有两个根;
当 时,方程有三个根
时,方程有三个根
分析:(1)利用f′(x)=3ax2+b的最小值为-12,可知b=-12,且a>0,根据直线6x+y+7=0的斜率为-6,可得f'(1)=3a+b=-6,所以a=2;
(2)由(1)知f(x)=2x3-12x, ,从而可求函数f(x)的单调增区间是(-∞,
,从而可求函数f(x)的单调增区间是(-∞, )和
)和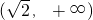 ,进而可知f(x)在
,进而可知f(x)在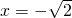 时取得极大值为
时取得极大值为 ,f(x)在
,f(x)在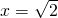 时取得极小值为
时取得极小值为 ,由此可确定方程解的情况.
,由此可确定方程解的情况.
点评:本题以导函数为载体,考查导数知识的应用,考查方程解的讨论,解题的关键是确定函数的极值,从而确定方程解的情况.
∴b=-12,且a>0
又直线6x+y+7=0的斜率为-6
∵函数f(x)=ax3+bx(a≠0)图象在点(1,f(1))处的切线与直线6x+y+7=0平行
∴f'(1)=3a+b=-6
∴a=2
∴a=2,b=-12
(2)由(1)知f(x)=2x3-12x,
 ,列表如下:
,列表如下:| x | (-∞, ) ) |  |  |  | 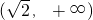 |
| f′ | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 )和
)和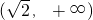
∴f(x)在
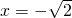 时取得极大值为
时取得极大值为 ,f(x)在
,f(x)在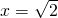 时取得极小值为
时取得极小值为
∴当
 或
或 时,方程有一根;
时,方程有一根;当
 或
或 时,方程有两个根;
时,方程有两个根;当
 时,方程有三个根
时,方程有三个根分析:(1)利用f′(x)=3ax2+b的最小值为-12,可知b=-12,且a>0,根据直线6x+y+7=0的斜率为-6,可得f'(1)=3a+b=-6,所以a=2;
(2)由(1)知f(x)=2x3-12x,
 ,从而可求函数f(x)的单调增区间是(-∞,
,从而可求函数f(x)的单调增区间是(-∞, )和
)和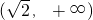 ,进而可知f(x)在
,进而可知f(x)在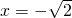 时取得极大值为
时取得极大值为 ,f(x)在
,f(x)在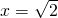 时取得极小值为
时取得极小值为 ,由此可确定方程解的情况.
,由此可确定方程解的情况.点评:本题以导函数为载体,考查导数知识的应用,考查方程解的讨论,解题的关键是确定函数的极值,从而确定方程解的情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目