题目内容
已知定义在R上的函数f(x),g(x)满足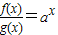 ,且f′(x)g(x)<f(x)g′(x),
,且f′(x)g(x)<f(x)g′(x),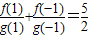 ,则a的值是( )
,则a的值是( )A.2
B.

C.3
D.

【答案】分析:根据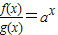 ,结合题中等式建立关于a的方程:a+
,结合题中等式建立关于a的方程:a+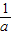 =
= ,解之得a=2或
,解之得a=2或 .再根据f′(x)g(x)<f(x)g′(x)可证出y=ax是R上的减函数,得a∈(0,1),由此可得a=
.再根据f′(x)g(x)<f(x)g′(x)可证出y=ax是R上的减函数,得a∈(0,1),由此可得a= .
.
解答:解:∵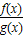 =ax,∴
=ax,∴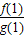 =a,
=a,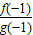 =a-1=
=a-1=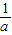
因此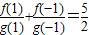 即a+
即a+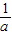 =
=
解之得a=2或
设F(x)=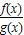 ,则F'(x)=
,则F'(x)=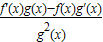
∵f'(x)g(x)<f(x)g'(x),
∴F'(x)=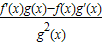 <0在R上成立,故F(x)是R上的减函数
<0在R上成立,故F(x)是R上的减函数
即y=ax是R上的减函数,故a∈(0,1)
所以实数a的值为
故选:B
点评:本题给出含有指数形式的函数,求解关于字母a的方程,着重考查了指数函数的单调性和导数的运算法则等知识,属于基础题.
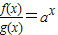 ,结合题中等式建立关于a的方程:a+
,结合题中等式建立关于a的方程:a+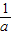 =
= ,解之得a=2或
,解之得a=2或 .再根据f′(x)g(x)<f(x)g′(x)可证出y=ax是R上的减函数,得a∈(0,1),由此可得a=
.再根据f′(x)g(x)<f(x)g′(x)可证出y=ax是R上的减函数,得a∈(0,1),由此可得a= .
.解答:解:∵
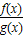 =ax,∴
=ax,∴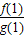 =a,
=a,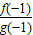 =a-1=
=a-1=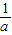
因此
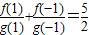 即a+
即a+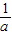 =
=
解之得a=2或

设F(x)=
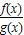 ,则F'(x)=
,则F'(x)=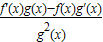
∵f'(x)g(x)<f(x)g'(x),
∴F'(x)=
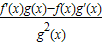 <0在R上成立,故F(x)是R上的减函数
<0在R上成立,故F(x)是R上的减函数即y=ax是R上的减函数,故a∈(0,1)
所以实数a的值为

故选:B
点评:本题给出含有指数形式的函数,求解关于字母a的方程,着重考查了指数函数的单调性和导数的运算法则等知识,属于基础题.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |