题目内容
计算由曲线y2=2x,直线y=x-4所围成的图形的面积.
解: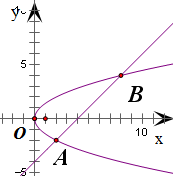 由方程组
由方程组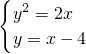 ,解之得
,解之得 或
或
∴曲线y2=2x与直线y=x-4交于点A(2,-2)和B(8,4).
因此,曲线y2=2x,直线y=x-4所围成的图形的面积为
S= +
+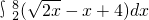
∵ =(
=( •
•
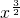 )
)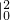 =
= ,
,
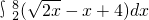 =(
=( •
•
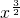 -
- x2+4x)
x2+4x)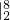
=( •
• •
•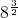 -
- ×82+4×8)-(
×82+4×8)-( •
• •
• -
- ×22+4×2)=
×22+4×2)=
∴所求图形面积为S= +
+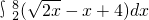 =
= +
+ =18
=18
分析:曲线y2=2x与直线y=x-4方程联解,得交点A(2,-2)、B(8,4).因此,所求图形面积为函数y=2 在[0,2]上的积分值,与函数y=
在[0,2]上的积分值,与函数y= -(x-4)在[2,8]上的积分值之和.利用公式分别算出这两个积分的值,相加即得所求图形的面积.
-(x-4)在[2,8]上的积分值之和.利用公式分别算出这两个积分的值,相加即得所求图形的面积.
点评:本题给出两条曲线,求它们围成图形的面积,着重考查了定积分计算公式和微积分基本定理等知识,属于中档题.
 由方程组
由方程组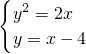 ,解之得
,解之得 或
或
∴曲线y2=2x与直线y=x-4交于点A(2,-2)和B(8,4).
因此,曲线y2=2x,直线y=x-4所围成的图形的面积为
S=
 +
+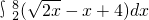
∵
 =(
=( •
•
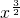 )
)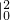 =
= ,
,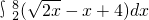 =(
=( •
•
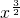 -
- x2+4x)
x2+4x)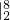
=(
 •
• •
•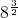 -
- ×82+4×8)-(
×82+4×8)-( •
• •
• -
- ×22+4×2)=
×22+4×2)=
∴所求图形面积为S=
 +
+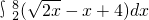 =
= +
+ =18
=18分析:曲线y2=2x与直线y=x-4方程联解,得交点A(2,-2)、B(8,4).因此,所求图形面积为函数y=2
 在[0,2]上的积分值,与函数y=
在[0,2]上的积分值,与函数y= -(x-4)在[2,8]上的积分值之和.利用公式分别算出这两个积分的值,相加即得所求图形的面积.
-(x-4)在[2,8]上的积分值之和.利用公式分别算出这两个积分的值,相加即得所求图形的面积.点评:本题给出两条曲线,求它们围成图形的面积,着重考查了定积分计算公式和微积分基本定理等知识,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目