题目内容
已知公差不为零的等差数列 的前
的前 项和
项和 ,且
,且 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足 ,求
,求 的前
的前 项和
项和 .
.
【答案】
(Ⅰ)根据题意把等差数列 的前
的前 项和关系式和
项和关系式和 成等比数列的关系式都表示成首项
成等比数列的关系式都表示成首项 和公差
和公差 的方程式,解方程组即可得数列
的方程式,解方程组即可得数列 的通项公式;(Ⅱ)由(Ⅰ)中
的通项公式;(Ⅱ)由(Ⅰ)中 的通项公式易知数列
的通项公式易知数列 的通项公式,再对式中
的通项公式,再对式中 分奇数和偶数两种情况讨论,分别求和,即得结论.
分奇数和偶数两种情况讨论,分别求和,即得结论.
【解析】
试题分析:(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
试题解析:(Ⅰ) 由已知得:
因为  所以
所以
 , 所以
, 所以  ,所以
,所以

所以  .
6分
.
6分
(Ⅱ) 
(ⅰ) 当 为奇数时,
为奇数时,

(ⅱ) 当 为偶数时,
为偶数时,
 ,
,
所以  . 14分
. 14分
考点:1、等差数列的通项和前 项和公式;2、等比数列的性质;3、等比数列的前
项和公式;2、等比数列的性质;3、等比数列的前 项和公式.
项和公式.

练习册系列答案
相关题目
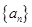 与公比为
与公比为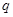 的等比数列
的等比数列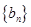 有相同的首项,同时满足
有相同的首项,同时满足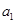 ,
,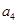 ,
,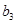 成等比,
成等比, ,
,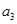 ,
,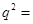 ( )
( )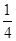 B.
B.
 C.
C.
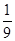 D.
D.