题目内容
(本题18分)已知数列![]() 的前
的前![]() 项和
项和![]() 和通项
和通项![]() 满足
满足![]() (
(![]() 是常数且
是常数且![]() ,
,![]() ).设函数
).设函数![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)当![]() 时,求
时,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 对
对![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解: (1)由题意,![]() ,得
,得![]()
![]() ∴
∴![]()
当![]() 时,
时, ![]() ,
,
![]() ∴
∴![]()
∴数列![]() 是首项
是首项![]() ,公比为
,公比为![]() 的等比数列,∴
的等比数列,∴![]()
(2) 由(1)知![]() ,
,![]()
当![]() 时,
时,![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)![]()
![]() ;
;
![]() ;
;
由![]() 得
得![]() ,
,
上式对![]() 都成立,所以
都成立,所以![]() ,又
,又![]() 为正整数,所以
为正整数,所以![]()
所以存在正整数![]() 使
使![]() 对
对![]() 都成立,其值为1,2,3.
都成立,其值为1,2,3.

练习册系列答案
相关题目
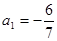 ,
,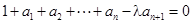 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),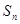 为数列{an}的前
为数列{an}的前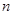 项和.
项和.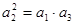 ,求
,求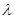 的值;
的值;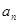 ;
;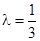 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由. 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足 ,
, .数列
.数列 满足
满足 .
.  时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
 是否可能恰为直线
是否可能恰为直线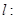
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由. 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足 ,
, .数列
.数列 满足
满足 .
.  时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
 是否可能恰为直线
是否可能恰为直线
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.