题目内容
已知偶函数f(x)满足条件:当x∈R时,恒有f(x+2)=f(x),且0≤x≤1时,有f′(x)>0,则f( ),f(
),f( ),f(
),f(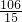 )的大小关系是
)的大小关系是
- A.f(
 )>f(
)>f( )>f(
)>f(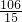 )
) - B.f(
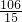 )>f(
)>f( )>f(
)>f( )
) - C.f(
 )>f(
)>f( )>f(
)>f(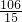 )
) - D.f(
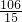 )>f(
)>f( )>f(
)>f( )
)
B
分析:0≤x≤1时,有f′(x)>0?f(x)在[0,1]上为增函数?在[-1,0]上为减函数?在[1,2]上为减函数,再把变量都转化到区间[1,2]上即可.
解答:∵0≤x≤1时,有f′(x)>0,∴f(x)在[0,1]上为增函数,
又∵f(x)是偶函数,∴在[-1,0]上为减函数,
由f(x+2)=f(x)得周期为2,所以f(x)在[1,2]上为减函数
又因为 =5
=5 ,
,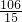 =7
=7 ,
, =5
=5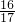 ,
,
所以f( )=f(1
)=f(1 ),f(
),f( )=f(1
)=f(1 ),f(
),f( )=f(1
)=f(1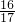 ),且1
),且1 <1
<1 <1
<1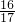
所以 f( )>f(
)>f( )>f(
)>f( )
)
故选 B.
点评:本题考查了函数的单调性,奇偶性和周期性.在利用单调性解题时遵循原则是:增函数自变量越大函数值越大,减函数自变量越小函数值越小.
分析:0≤x≤1时,有f′(x)>0?f(x)在[0,1]上为增函数?在[-1,0]上为减函数?在[1,2]上为减函数,再把变量都转化到区间[1,2]上即可.
解答:∵0≤x≤1时,有f′(x)>0,∴f(x)在[0,1]上为增函数,
又∵f(x)是偶函数,∴在[-1,0]上为减函数,
由f(x+2)=f(x)得周期为2,所以f(x)在[1,2]上为减函数
又因为
 =5
=5 ,
,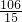 =7
=7 ,
, =5
=5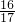 ,
,所以f(
 )=f(1
)=f(1 ),f(
),f( )=f(1
)=f(1 ),f(
),f( )=f(1
)=f(1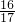 ),且1
),且1 <1
<1 <1
<1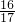
所以 f(
 )>f(
)>f( )>f(
)>f( )
)故选 B.
点评:本题考查了函数的单调性,奇偶性和周期性.在利用单调性解题时遵循原则是:增函数自变量越大函数值越大,减函数自变量越小函数值越小.

练习册系列答案
相关题目