题目内容
对于正整数a,b,存在唯一一对整数q和r,使得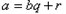 ,
,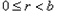 .特别地,当
.特别地,当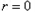 时,称b能整除a,记作
时,称b能整除a,记作 ,已知
,已知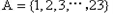
(1)存在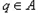 ,使得
,使得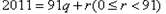 ,试求
,试求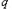 ,
, 的值;
的值;
(2)求证:不存在这样的函数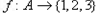 ,使得对任意的整数
,使得对任意的整数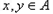 ,若
,若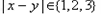 ,则
,则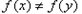 ;
;
(3)若 ,
,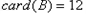 (
(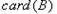 指集合B中的元素的个数),且存在
指集合B中的元素的个数),且存在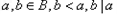 ,则称
,则称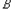 为“和谐集”,.求最大的
为“和谐集”,.求最大的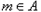 ,使含m的集合A的有12个元素的任意子集为“和谐集”,并说明理由.
,使含m的集合A的有12个元素的任意子集为“和谐集”,并说明理由.
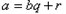 ,
,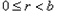 .特别地,当
.特别地,当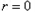 时,称b能整除a,记作
时,称b能整除a,记作 ,已知
,已知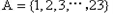
(1)存在
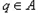 ,使得
,使得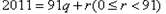 ,试求
,试求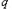 ,
, 的值;
的值;(2)求证:不存在这样的函数
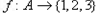 ,使得对任意的整数
,使得对任意的整数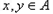 ,若
,若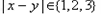 ,则
,则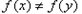 ;
;(3)若
 ,
,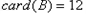 (
(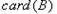 指集合B中的元素的个数),且存在
指集合B中的元素的个数),且存在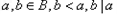 ,则称
,则称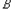 为“和谐集”,.求最大的
为“和谐集”,.求最大的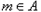 ,使含m的集合A的有12个元素的任意子集为“和谐集”,并说明理由.
,使含m的集合A的有12个元素的任意子集为“和谐集”,并说明理由.解:(1)因为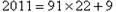 ,
,
所以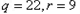 .
.
(2)证明:假设存在这样的函数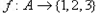 ,使得对任意的整数
,使得对任意的整数 ,
,
若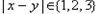 ,则
,则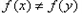 .
.
设 ,
,
由已知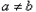 ,由于
,由于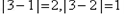 ,
,
所以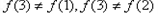 .
.
不妨令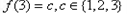 ,这里
,这里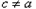 ,且
,且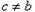 ,
,
同理,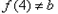 ,且
,且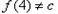 ,
,
因为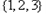 只有三个元素,
只有三个元素,
所以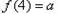 .即
.即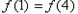 ,
,
但是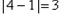 ,与已知矛盾.
,与已知矛盾.
因此假设不成立,即不存在这样的函数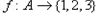 ,使得对任意的整数
,使得对任意的整数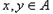 ,
,
若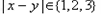 ,则
,则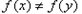 .
.
(3)当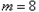 时,记
时,记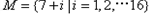 ,
,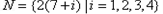 ,
,
记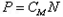 ,则
,则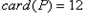 ,
,
显然对任意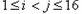 ,不存在
,不存在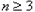 ,使得
,使得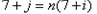 成立.
成立.
故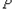 是非“和谐集”,此时
是非“和谐集”,此时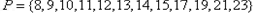 .
.
同样的,当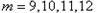 时,存在含
时,存在含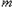 的集合
的集合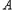 的有12个元素的子集为非“和谐集”.
的有12个元素的子集为非“和谐集”.
因此m≤7
下面证明:含7的任意集合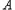 的有12个元素的子集为“和谐集”.
的有12个元素的子集为“和谐集”.
设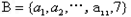 ,若
,若 中之一为集合
中之一为集合 的元素,
的元素,
显然为”.现考虑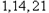 都不属于集合
都不属于集合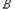 ,构造集合
,构造集合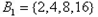 ,
,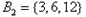 ,
,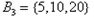 ,
,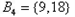 ,
,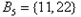 ,
,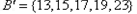 .
.
以上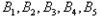 每个集合中的元素都是倍数关系.
每个集合中的元素都是倍数关系.
考虑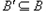 的情况,也即
的情况,也即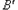 中5个元素全都是
中5个元素全都是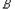 的元素,
的元素,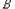 中剩下6个元素必须从
中剩下6个元素必须从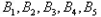 这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,
这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,
即集合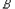 中至少有两个元素存在倍数关系.
中至少有两个元素存在倍数关系.
综上所述,含7的任意集合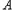 的有12个元素的子集
的有12个元素的子集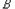 为”,即
为”,即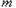 的最大值为7.
的最大值为7.
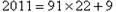 ,
,所以
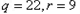 .
. (2)证明:假设存在这样的函数
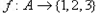 ,使得对任意的整数
,使得对任意的整数 ,
,若
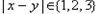 ,则
,则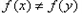 .
. 设
 ,
,由已知
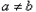 ,由于
,由于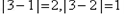 ,
,所以
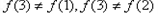 .
. 不妨令
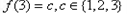 ,这里
,这里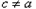 ,且
,且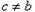 ,
,同理,
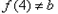 ,且
,且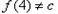 ,
,因为
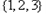 只有三个元素,
只有三个元素,所以
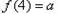 .即
.即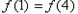 ,
,但是
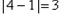 ,与已知矛盾.
,与已知矛盾.因此假设不成立,即不存在这样的函数
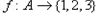 ,使得对任意的整数
,使得对任意的整数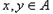 ,
,若
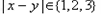 ,则
,则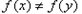 .
. (3)当
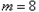 时,记
时,记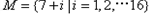 ,
,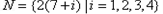 ,
,记
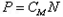 ,则
,则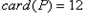 ,
,显然对任意
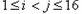 ,不存在
,不存在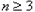 ,使得
,使得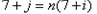 成立.
成立.故
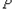 是非“和谐集”,此时
是非“和谐集”,此时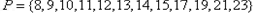 .
.同样的,当
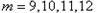 时,存在含
时,存在含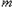 的集合
的集合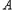 的有12个元素的子集为非“和谐集”.
的有12个元素的子集为非“和谐集”. 因此m≤7
下面证明:含7的任意集合
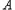 的有12个元素的子集为“和谐集”.
的有12个元素的子集为“和谐集”.设
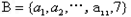 ,若
,若 中之一为集合
中之一为集合 的元素,
的元素,显然为”.现考虑
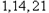 都不属于集合
都不属于集合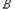 ,构造集合
,构造集合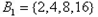 ,
,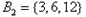 ,
,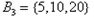 ,
,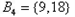 ,
,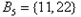 ,
,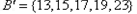 .
.以上
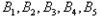 每个集合中的元素都是倍数关系.
每个集合中的元素都是倍数关系.考虑
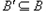 的情况,也即
的情况,也即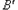 中5个元素全都是
中5个元素全都是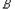 的元素,
的元素,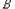 中剩下6个元素必须从
中剩下6个元素必须从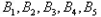 这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,
这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,即集合
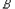 中至少有两个元素存在倍数关系.
中至少有两个元素存在倍数关系.综上所述,含7的任意集合
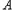 的有12个元素的子集
的有12个元素的子集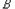 为”,即
为”,即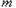 的最大值为7.
的最大值为7. 
练习册系列答案
相关题目