题目内容
已知函数f(x)= +cx+d(a,c,d∈R)满足f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立.
+cx+d(a,c,d∈R)满足f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立.
(1)求a,c,d的值;
(2)若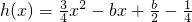 ,解不等式f'(x)+h(x)<0;
,解不等式f'(x)+h(x)<0;
(3)是否存在实数m,使函数g(x)=f'(x)-mx在区间[m,m+2]上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
解:(1)∵f(0)=0,∴d=0
∴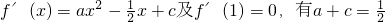
∵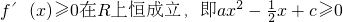 恒成立
恒成立
显然a=0时,上式不能恒成立∴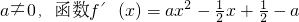 是二次函数
是二次函数
由于对一切x∈R,都有f'(x)≥0,于是由二次函数的性质可得
即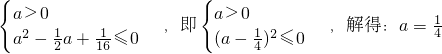
 .
.
(2)∵ ∴
∴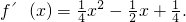
∴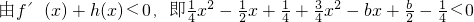
即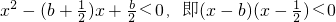
当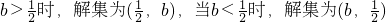 ,当
,当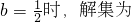 .
.
(3)∵ ,∴
,∴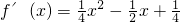
∴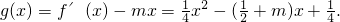
该函数图象开口向上,且对称轴为x=2m+1.
假设存在实数m使函数 区间[m.m+2]上有最小值-5.
区间[m.m+2]上有最小值-5.
①当m<-1时,2m+1<m,函数g(x)在区间[m,n+2]上是递增的.
∴
解得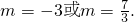 ∵
∵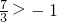 ,∴
,∴ 舍去
舍去
②当-1≤m<1时,m≤2m+1<m+2,函数g(x)在区间[m,2m+1]上是递减的,
而在区间[2m+1,m+2]上是递增的,∴g(2m+1)=-5.
即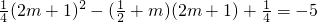
解得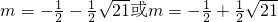 ,均应舍去
,均应舍去
③当m≥1时,2m+1≥m+2,函数g(x)在区间[m,m+2]上递减的∴g(m+2)=-5
即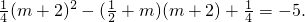
解得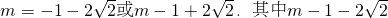 应舍去.
应舍去.
综上可得,当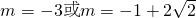 时,
时,
函数g(x)=f'(x)-mx在区间[m,m+2]上有最小值-5.
分析:(1)待定系数法求函数解析式,由f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立列出三个方程,解出a、b、c
(2)一元二次不等式解法,注意根之间比较,考查分类讨论思想
(3)考查二次函数最值问题,考查分类讨论思想,对m进行讨论,看对称轴与区间的关系.
点评:本题考查导数的综合运用,具体包含导数的计算、恒成立问题、不等式的解法、待定系数法求函数解析式、二次函数最值问题,分类讨论思想,对学生有一定的能力要求,属于难题.
∴
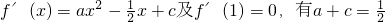
∵
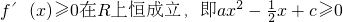 恒成立
恒成立显然a=0时,上式不能恒成立∴
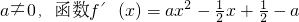 是二次函数
是二次函数由于对一切x∈R,都有f'(x)≥0,于是由二次函数的性质可得

即
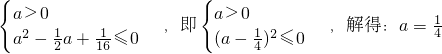
 .
.(2)∵
 ∴
∴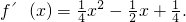
∴
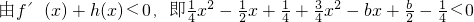
即
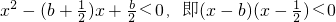
当
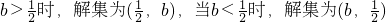 ,当
,当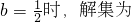 .
.(3)∵
 ,∴
,∴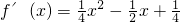
∴
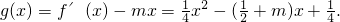
该函数图象开口向上,且对称轴为x=2m+1.
假设存在实数m使函数
 区间[m.m+2]上有最小值-5.
区间[m.m+2]上有最小值-5.①当m<-1时,2m+1<m,函数g(x)在区间[m,n+2]上是递增的.
∴

解得
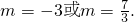 ∵
∵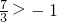 ,∴
,∴ 舍去
舍去②当-1≤m<1时,m≤2m+1<m+2,函数g(x)在区间[m,2m+1]上是递减的,
而在区间[2m+1,m+2]上是递增的,∴g(2m+1)=-5.
即
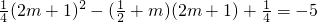
解得
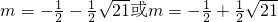 ,均应舍去
,均应舍去③当m≥1时,2m+1≥m+2,函数g(x)在区间[m,m+2]上递减的∴g(m+2)=-5
即
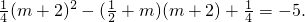
解得
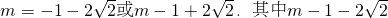 应舍去.
应舍去.综上可得,当
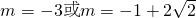 时,
时,函数g(x)=f'(x)-mx在区间[m,m+2]上有最小值-5.
分析:(1)待定系数法求函数解析式,由f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立列出三个方程,解出a、b、c
(2)一元二次不等式解法,注意根之间比较,考查分类讨论思想
(3)考查二次函数最值问题,考查分类讨论思想,对m进行讨论,看对称轴与区间的关系.
点评:本题考查导数的综合运用,具体包含导数的计算、恒成立问题、不等式的解法、待定系数法求函数解析式、二次函数最值问题,分类讨论思想,对学生有一定的能力要求,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|