题目内容
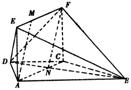
(12分)如图,在梯形ABCD中![]() ,平面
,平面![]() 平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
(Ⅰ)求证:![]() 平面ACFE;
平面ACFE;
(Ⅱ)当EM为何值时,![]() 平面BDF?证明你的结论;
平面BDF?证明你的结论;
(Ⅲ)求二面角B―EF―D的大小.

![]()
解析:(Ⅰ)在梯形ABCD中,∵![]() ,
,
∴四边形ABCD是等腰梯形,
且![]()
∴![]() ,∴
,∴![]()
又∵平面![]() 平面ABCD,交线为AC,∴
平面ABCD,交线为AC,∴![]() 平面ACFE.
平面ACFE.
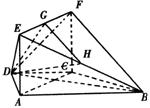
(Ⅱ)当![]() 时,
时,![]() 平面BDF. 在梯形ABCD中,设
平面BDF. 在梯形ABCD中,设![]() ,连结FN,则
,连结FN,则![]()
∵![]() 而
而![]() ,∴
,∴![]() ∴MF
∴MF![]() AN,
AN,
∴四边形ANFM是平行四边形. ∴![]()
又∵![]() 平面BDF,
平面BDF,![]() 平面BDF. ∴
平面BDF. ∴![]() 平面BDF.
平面BDF.
(Ⅲ)取EF中点G,EB中点H,连结DG、GH、DH,∵DE=DF,∴![]() ∵
∵![]() 平面ACFE,∴
平面ACFE,∴![]() 又∵
又∵![]() ,∴
,∴![]() 又∵
又∵![]() ,∴
,∴![]()
∴![]() 是二面角B―EF―D的平面角.
是二面角B―EF―D的平面角.
在△BDE中![]() ∴
∴![]() ∴
∴![]() ,
,
![]()
![]() ∴
∴![]() 又
又![]() ∴在△DGH中,
∴在△DGH中,

练习册系列答案
相关题目
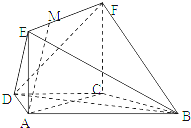 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.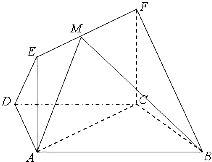 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.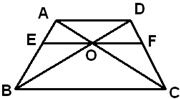 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.