题目内容
设无穷等差数列{an}的前n项和为Sn。
(1)若首项a1= ,公差d=1,求满足
,公差d=1,求满足 的正整数k;
的正整数k;
(2)求所有的无穷等差数列{an},使得对于一切正整数k都有 成立。
成立。
(1)若首项a1=
 ,公差d=1,求满足
,公差d=1,求满足 的正整数k;
的正整数k;(2)求所有的无穷等差数列{an},使得对于一切正整数k都有
 成立。
成立。解:(1) ;
;
(2) 或
或 或
或
则共有3个满足条件的无穷等差数列:
{an}:an=0,即0,0,0,…
{an}:an=1,即1,1,1,…
{an}:an=2n-1。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,公差d=1.求满足
,公差d=1.求满足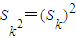 的正整数k;
的正整数k;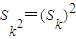 成立.
成立.