题目内容
16.已知数列{an}的前n项和为Sn,且Sn=n2+2n,(n∈N*).(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设集合A={x|x=2n+2,n∈N*},B={x|x=2an,n∈N*},等差数列{cn}的任一项cn∈A∩B,其中c1是A∩B中的最小数,110<c10<115,求数列{cn}的通项公式.
分析 (Ⅰ)利用an=Sn-Sn-1计算并验证即可;
(Ⅱ)通过A、B间的包含关系可得c1=6,从而可得${c_{10}}=4m+6(m∈{N^*})$,利用110<c10<115,可得c10=114,根据等差数列的性质计算即可.
解答 解:(Ⅰ)∵${S_n}={n^2}+2n,(n∈{N^*})$.
当n≥2时,an=Sn-Sn-1=2n+1,
当n=1时,a1=S1=3满足上式,
所以数列{an}的通项公式为an=2n+1;
(Ⅱ)∵A={x|x=2n+2,n∈N*},B={x|x=4n+2,n∈N*},∴A∩B=B.
又∵cn∈A∩B,其中c1是A∩B中的最小数,∴c1=6,
∵{cn}的公差是4的倍数,∴${c_{10}}=4m+6(m∈{N^*})$.
又∵110<c10<115,
解得m=27,所以c10=114,
设等差数列的公差为d,
则$d=\frac{{{c_{10}}-{c_1}}}{10-1}=\frac{114-6}{9}=12$,
∴cn=6+(n-1)12=12n-6,
所以{cn}的通项公式为cn=12n-6.
点评 本题考查数列的基本性质,通项公式,集合的交集及其运算,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
6.执行如图所示的程序框图,若P=$\frac{11}{12}$.则输出的n=( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
4.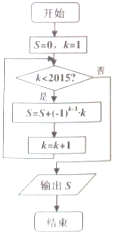 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )
 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )| A. | -1008 | B. | -1007 | C. | 1007 | D. | 1008 |