题目内容
已知椭圆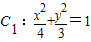
和抛物线C2：y2=2px（p＞0），过点M（1，0）且倾斜角为
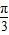的直线与抛物线交于A、B，与椭圆交于C、D，当|AB|：|CD|=5：3时，求p的值．
【答案】分析：先设出直线的参数方程，别代入椭圆、抛物线方程的到关于t的一元二次方程，设A、B、C、D的参数分别为t1、t2、t3、t4，利用根据与系数关系表示出|AB|：|CD|，从而得到所求．
解答：
解：设直线方程是
，分别代入椭圆、抛物线方程得：
5t2+4t-12=0（1）3t2-4pt-8p=0（2）
设A、B、C、D的参数分别为t1、t2、t3、t4，
则
，
，由|AB|：|CD|=5：3解得p=2．
点评：本题主要考查了直线与椭圆和抛物线之间的有关问题，求解圆锥曲线的综合题需画出图形理解题意，同时考查了直线的参数方程，以及参数方程的几何意义，属于中档题．
解答：
解：设直线方程是，分别代入椭圆、抛物线方程得：5t2+4t-12=0（1）3t2-4pt-8p=0（2）
设A、B、C、D的参数分别为t1、t2、t3、t4，
则
，，由|AB|：|CD|=5：3解得p=2．点评：本题主要考查了直线与椭圆和抛物线之间的有关问题，求解圆锥曲线的综合题需画出图形理解题意，同时考查了直线的参数方程，以及参数方程的几何意义，属于中档题．
练习册系列答案
相关题目
已知椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点O，从每条曲线上取两个点，将其坐标记录于下表中：
则C1、C2的标准方程分别为 、 ．
| C1 | C2 | |||||||||
| x | 2 |
|
4 | 3 | ||||||
| y | 0 |
|
4 | -2
| ||||||
和抛物线C2∶y2＝2px(p＞0)，过点M(1，0)且倾斜角为
的直线与抛物线交于A、B，与椭圆交于C、D，当|AB|∶|CD|＝5∶3时，求p的值．