题目内容
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
(Ⅰ)证明:AC⊥A1B;
(Ⅱ)求几何体C1DABA1的体积。
(Ⅰ)证明:AC⊥A1B;
(Ⅱ)求几何体C1DABA1的体积。
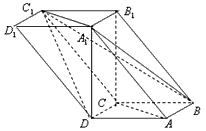
(Ⅰ)证明:连结BD交AC于点O,
∵四边形ABCD是正方形,
∴AC⊥BD,
又∵AD1⊥平面ABCD,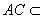 平面ABCD,
平面ABCD,
∴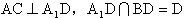 ,
,
∴AC⊥平面A1BD,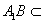 平面A1BD,
平面A1BD,
∴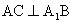 。
。
(Ⅱ)解: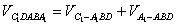 ,
,
∵AD1⊥平面ABCD,
∴AD1为几何体A1-ABD的高,
∴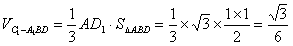 ,
,
∵四棱柱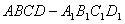 ,
,
∴CC1∥AA1,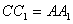 ,
,
∴四边形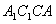 是平行四边形,
是平行四边形,
∴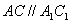 ,由(1)得AC⊥平面A1BD,
,由(1)得AC⊥平面A1BD,
∴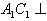 平面A1BD,
平面A1BD,
∴A1C1为几何体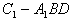 的高,
的高,
∵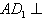 平面ABCD,
平面ABCD,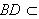 平面ABCD,
平面ABCD,
∴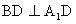 ,
,
∴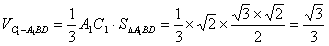 ,
,
∴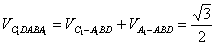 。
。
∵四边形ABCD是正方形,
∴AC⊥BD,
又∵AD1⊥平面ABCD,
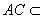 平面ABCD,
平面ABCD,∴
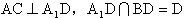 ,
,∴AC⊥平面A1BD,
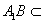 平面A1BD,
平面A1BD,∴
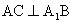 。
。 (Ⅱ)解:
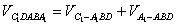 ,
, ∵AD1⊥平面ABCD,
∴AD1为几何体A1-ABD的高,
∴
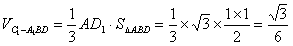 ,
, ∵四棱柱
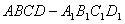 ,
,∴CC1∥AA1,
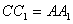 ,
,∴四边形
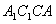 是平行四边形,
是平行四边形, ∴
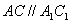 ,由(1)得AC⊥平面A1BD,
,由(1)得AC⊥平面A1BD,∴
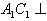 平面A1BD,
平面A1BD,∴A1C1为几何体
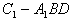 的高,
的高,∵
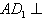 平面ABCD,
平面ABCD,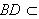 平面ABCD,
平面ABCD,∴
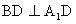 ,
,∴
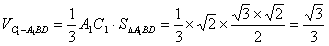 ,
,∴
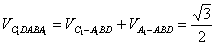 。
。
练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
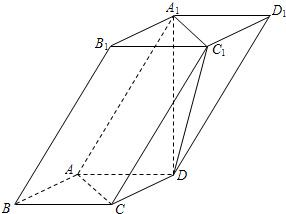 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.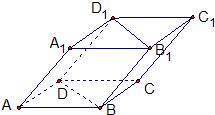 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是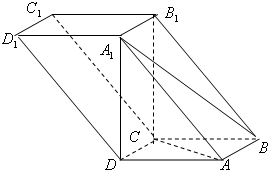 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2, (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD. (2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,