题目内容
.(本小题满分14分)
设 实数
实数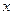 、
、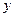 同时满足条件:
同时满足条件: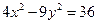 ,且
,且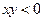 ,
,
(1)求函数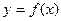 的解析式和定义域;
的解析式和定义域;
(2)判断函数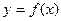 的奇偶性;
的奇偶性;
(3)若方程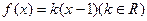 恰有两个不同的实数根,求
恰有两个不同的实数根,求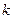 的取值范围
的取值范围
设
 实数
实数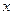 、
、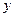 同时满足条件:
同时满足条件: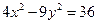 ,且
,且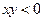 ,
,(1)求函数
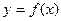 的解析式和定义域;
的解析式和定义域;(2)判断函数
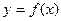 的奇偶性;
的奇偶性;(3)若方程
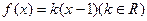 恰有两个不同的实数根,求
恰有两个不同的实数根,求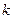 的取值范围
的取值范围解:(1)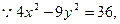
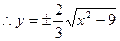 .……………………………………… 1分
.……………………………………… 1分
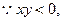
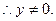
又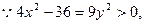
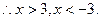
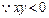 ,
,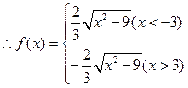 .……………………………………… 3分
.……………………………………… 3分
函数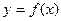 的定义域为集合D=
的定义域为集合D=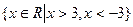 .……………………… 4分
.……………………… 4分
(2)当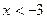 有
有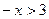 ,
,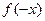 =
=

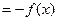 ……… 5分
……… 5分
同理,当 时,有
时,有 .…………………………………………… 6分
.…………………………………………… 6分
任设 ,有
,有 …………………………………………………………… 7分
…………………………………………………………… 7分
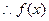 为定义域上的奇数.……………………………………………………… 8分
为定义域上的奇数.……………………………………………………… 8分
(3) 联立方程组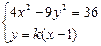 可得,
可得,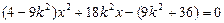 ………… 9分
………… 9分
(Ⅰ)当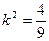 时,即
时,即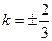 时,方程只有唯一解,与题意
时,方程只有唯一解,与题意 不符; ………………… 10分
不符; ………………… 10分
(Ⅱ)当 时,即方程为一个一元二次方程,
时,即方程为一个一元二次方程,
要使方程有两个相异实数根,则
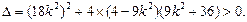
解之得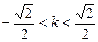 , ……………………………………………………… 12分
, ……………………………………………………… 12分
但由于函数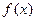 的图象在第二、四象限。……………………………………… 13分
的图象在第二、四象限。……………………………………… 13分
故直线的斜率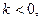 综上可知
综上可知 或
或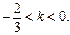 ………………… 14分
………………… 14分
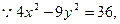
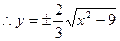 .……………………………………… 1分
.……………………………………… 1分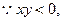
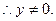
又
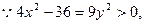
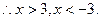
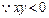 ,
,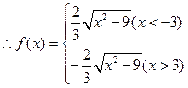 .……………………………………… 3分
.……………………………………… 3分函数
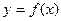 的定义域为集合D=
的定义域为集合D=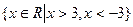 .……………………… 4分
.……………………… 4分(2)当
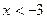 有
有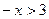 ,
,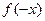 =
=

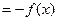 ……… 5分
……… 5分同理,当
 时,有
时,有 .…………………………………………… 6分
.…………………………………………… 6分任设
 ,有
,有 …………………………………………………………… 7分
…………………………………………………………… 7分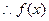 为定义域上的奇数.……………………………………………………… 8分
为定义域上的奇数.……………………………………………………… 8分(3) 联立方程组
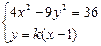 可得,
可得,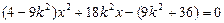 ………… 9分
………… 9分(Ⅰ)当
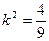 时,即
时,即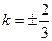 时,方程只有唯一解,与题意
时,方程只有唯一解,与题意 不符; ………………… 10分
不符; ………………… 10分(Ⅱ)当
 时,即方程为一个一元二次方程,
时,即方程为一个一元二次方程,要使方程有两个相异实数根,则
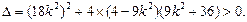
解之得
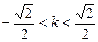 , ……………………………………………………… 12分
, ……………………………………………………… 12分但由于函数
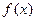 的图象在第二、四象限。……………………………………… 13分
的图象在第二、四象限。……………………………………… 13分故直线的斜率
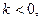 综上可知
综上可知 或
或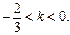 ………………… 14分
………………… 14分略

练习册系列答案
相关题目
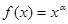 的图像经过点(2,4),则下列命题中不正确的是( )
的图像经过点(2,4),则下列命题中不正确的是( )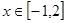 时,函数
时,函数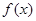 取值范围是
取值范围是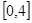
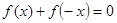
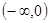
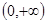 上单调递增的是
上单调递增的是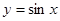
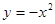
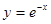
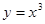
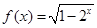 的定义域是 ( )
的定义域是 ( )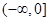
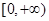
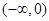
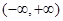
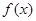 为定义在R上的奇函数,当
为定义在R上的奇函数,当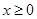 时,
时,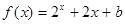 (b为常数),
(b为常数),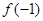 等于( )
等于( )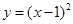
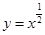
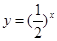
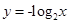
 ,
,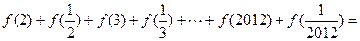 .
.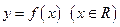 满足
满足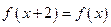 且
且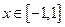 时,
时,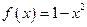 ,函数
,函数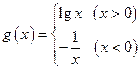 ,则函数
,则函数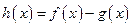 在区间
在区间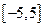 内的零点的个数为
内的零点的个数为