题目内容
如果函数 (a>0)没有零点,则a的取值范围为
(a>0)没有零点,则a的取值范围为
- A.(0,1)
- B.(0,1)

- C.(0,1)∪(2,+∞)
- D.
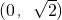 ∪(2,+∞)
∪(2,+∞)
C
分析:根据函数 (a>0)没有零点,即函数y=
(a>0)没有零点,即函数y= 与y=
与y= 的图象没有交点,在同一坐标系中画出它们的图象,即可求出a的取值范围.
的图象没有交点,在同一坐标系中画出它们的图象,即可求出a的取值范围.
解答:令 ,得
,得
令y= 是半径为
是半径为 圆心在原点的圆的上半部分,y=
圆心在原点的圆的上半部分,y= 以(0,
以(0, )端点的折线,在同一坐标系中画出它们的图象:如图,根据图象知,由于两曲线没有公共点,故圆到折线的距离小于1,或者圆心到折线的距离大于半径
)端点的折线,在同一坐标系中画出它们的图象:如图,根据图象知,由于两曲线没有公共点,故圆到折线的距离小于1,或者圆心到折线的距离大于半径
∴a的取值范围为(0,1)∪(2,+∞)
故选C.
点评:此题考查函数零点与函数图象的交点之间的关系,体现了转化的数学思想方法,属中档题.
分析:根据函数
 (a>0)没有零点,即函数y=
(a>0)没有零点,即函数y= 与y=
与y= 的图象没有交点,在同一坐标系中画出它们的图象,即可求出a的取值范围.
的图象没有交点,在同一坐标系中画出它们的图象,即可求出a的取值范围.解答:令
 ,得
,得
令y=
 是半径为
是半径为 圆心在原点的圆的上半部分,y=
圆心在原点的圆的上半部分,y= 以(0,
以(0, )端点的折线,在同一坐标系中画出它们的图象:如图,根据图象知,由于两曲线没有公共点,故圆到折线的距离小于1,或者圆心到折线的距离大于半径
)端点的折线,在同一坐标系中画出它们的图象:如图,根据图象知,由于两曲线没有公共点,故圆到折线的距离小于1,或者圆心到折线的距离大于半径
∴a的取值范围为(0,1)∪(2,+∞)
故选C.

点评:此题考查函数零点与函数图象的交点之间的关系,体现了转化的数学思想方法,属中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目