题目内容
若函数f(x)是偶函数,且在(0,+∞)内是增函数,又f(-3)=0.则x•f(x)<0的解集是________.
(-∞,-3)∪(0,3)
分析:先利用f(x)是偶函数单调性在对称区间上相反,分析出函数的单调性,结合f(-3)=0,分析出函数在各个区间上的符号,进而得到x•f(x)<0的解集
解答:∵函数f(x)是偶函数,且在(0,+∞)内是增函数,
∴f(x)在(-∞,0)内是减函数
又∵f(-3)=f(3)=0
∴f(x)<0的解集是(-3,3),f(x)>0的解集是(-∞,-3),(3,+∞)
∴x•f(x)<0的解集为(-∞,-3)∪(0,3)
故答案为:(-∞,-3)∪(0,3)
点评:本题考查的知识点是函数奇偶性与函数的单调性,其中根据偶函数单调性在对称区间上相反,分析出函数的单调性,是解答的关键.
分析:先利用f(x)是偶函数单调性在对称区间上相反,分析出函数的单调性,结合f(-3)=0,分析出函数在各个区间上的符号,进而得到x•f(x)<0的解集
解答:∵函数f(x)是偶函数,且在(0,+∞)内是增函数,
∴f(x)在(-∞,0)内是减函数
又∵f(-3)=f(3)=0
∴f(x)<0的解集是(-3,3),f(x)>0的解集是(-∞,-3),(3,+∞)
∴x•f(x)<0的解集为(-∞,-3)∪(0,3)
故答案为:(-∞,-3)∪(0,3)
点评:本题考查的知识点是函数奇偶性与函数的单调性,其中根据偶函数单调性在对称区间上相反,分析出函数的单调性,是解答的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
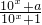 是奇函数.
是奇函数.