题目内容
用“<”号把三个数a=(
)
,b=(
)
,c=(
)
连接起来的是
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
a<b<c
a<b<c
.分析:y=x
在第一象限是增函数,且
<
,所以a=(
)
<c=(
)
,因为y=(
)x是减函数,且
<
,所以b=(
)
>c=(
)
.由此能比较三个数a=(
)
,b=(
)
,c=(
)
的大小.
| 2 |
| 5 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
解答:解:∵y=x
在第一象限是增函数,
且
<
,
∴a=(
)
<c=(
)
,
∵y=(
)x是减函数,
且
<
,
∴b=(
)
>c=(
)
.
∴a<b<c.
故答案为a<b<c.
| 2 |
| 5 |
且
| 1 |
| 5 |
| 1 |
| 2 |
∴a=(
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
∵y=(
| 1 |
| 2 |
且
| 1 |
| 3 |
| 2 |
| 5 |
∴b=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
∴a<b<c.
故答案为a<b<c.
点评:本题考查指数式大小的比较,是基础题.解题时要认真审题,注意幂函数和指数函数单调性的灵活运用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量 .
. 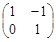 ,点O(0,0),M(2,-1),N(0,2),求
,点O(0,0),M(2,-1),N(0,2),求 在矩阵AB的对应变换作用下所得到的
在矩阵AB的对应变换作用下所得到的 的面积.
的面积.  的参数方程为
的参数方程为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 .
. ,不等式
,不等式 在
在 上恒成立.
上恒成立. 的取值范围;
的取值范围; ,若正实数
,若正实数 满足
满足 ,求
,求 的最大值.
的最大值.