题目内容
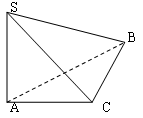
如图，在三棱锥S-ABC中，∠ACB=90°，SA⊥面ABC，AC=2，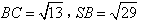
，
，
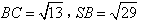（1）证明SC⊥BC；
（2）求侧面SBC与底面ABC所成二面角的大小。
（2）求侧面SBC与底面ABC所成二面角的大小。
（1）证明：∵∠SAB=∠SCA=90°，
∴
，
，
又
，
∴
，
由于∠ACB=90°，即
，
由三垂线定理，得
。
（2）解：
，
∴∠SCA是侧面SBC与底面ABC所成二面角的平面角，
在Rt△SCB中，由于
，
在Rt△SAC中，由于AC=2，SC=4，
∴
，
∴
，
即
为60°。
∴
，，又
，∴
，由于∠ACB=90°，即
，由三垂线定理，得
。（2）解：
，∴∠SCA是侧面SBC与底面ABC所成二面角的平面角，
在Rt△SCB中，由于
，在Rt△SAC中，由于AC=2，SC=4，
∴
，∴
，即
为60°。 
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在三棱锥S-ABC中，SA⊥平面ABC，平面SAB⊥平面SBC．
如图，在三棱锥S-ABC中，G1，G2分别是△SAB和△SAC的重心，则直线G1G2与BC的位置关系是（ ）
如图，在三棱锥S-ABC中，平面SBC⊥平面ABC，SB=SC=AB=2，BC=2
（2013•杭州模拟）如图，在三棱锥S-ABC中，SA=SC=AB=BC，则直线SB与AC所成角的大小是（ ）
（2013•成都一模）如图，在三棱锥S-ABC中，SA丄平面ABC，SA=3，AC=2，AB丄BC，点P是SC的中点，则异面直线SA与PB所成角的正弦值为（ ）