题目内容
已知点G是△ABC的重心,A(0,-1),B(0,1).在x轴上有一点M,满足|(1)求点C的轨迹E的方程;
(2)若斜率为k的直线l与(1)中的曲线E交于不同的两点P、Q,且|![]() |=|
|=|![]() |,试求斜率k的取值范围.
|,试求斜率k的取值范围.
解:(1)设C(x,y),则G(![]() ,
,![]() ).
).
∵![]() =λ
=λ![]() (λ∈R),∴GM∥AB.又M是x轴上一点,则M(
(λ∈R),∴GM∥AB.又M是x轴上一点,则M(![]() ,0).又∵|
,0).又∵|![]() |=|
|=|![]() |,
|,
∴(![]() =
=![]() .
.
整理,得![]() +y2=1(x≠0).
+y2=1(x≠0).
(2)①当k=0时,l与椭圆C有两个不同的交点P、Q,
根据椭圆的对称性,有|AP|=|AQ|,符合题意.
②当k≠0时,可设l的方程为y=kx+m,联立方程组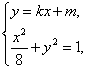 消去y整理,得
消去y整理,得
(1+3k2)x2+6kmx+3(m2-1)=0.(*)
∵直线l和椭圆交于不同的两点,
∴Δ=(6km)2-4(1+3k2)×3(m2-1)>0,
即1+3k2-m2>0.(**)
设P(x1,y1),Q(x2,y2),则x1、x2是方程(*)的两相异实根.
∴x1+x2=![]() ,x1·x2=
,x1·x2=![]() .
.
则PQ的中点N(x0,y0)的坐标是x0=![]() ,y0=
,y0=![]() ,
,
即N(![]() ,
,![]() ).又|
).又|![]() |=|
|=|![]() |,
|,
∴AN⊥PQ.∴m=![]() .将m=
.将m=![]() 代入(**)式,得k2<1.∴k∈(-1,0)∪(0,1).
代入(**)式,得k2<1.∴k∈(-1,0)∪(0,1).
综上①②,得k的取值范围是(-1,1).

练习册系列答案
相关题目
已知点G是△ABC的重心,点P是△GBC内一点,若
=λ
+μ
,则λ+μ的取值范围是( )
| AP |
| AB |
| AC |
A、(
| ||
B、(
| ||
C、(1,
| ||
| D、(1,2) |