题目内容
对任意的实数x,不等式mx2-mx-1<0恒成立,则实数m的取值范围是( )
| A.(-4,0) | B.(-4,0] | C.[-4,0] | D.[-4,0) |
当m=0时,mx2-mx-1=-1<0,不等式成立;
设y=mx2-mx-1,当m≠0时函数y为二次函数,y要恒小于0,抛物线开口向下且与x轴没有交点,即要m<0且△<0
得到:
解得-4<m<0.
综上得到-4<m≤0.
故选B.
设y=mx2-mx-1,当m≠0时函数y为二次函数,y要恒小于0,抛物线开口向下且与x轴没有交点,即要m<0且△<0
得到:
|
综上得到-4<m≤0.
故选B.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 则f1(x)∈M;
则f1(x)∈M;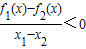 ;
;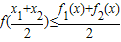 .
.