题目内容
用红、黄、蓝三种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,求: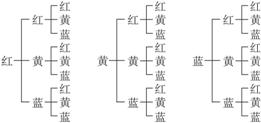
(1)3个矩形颜色都相同的概率;
(2)3个矩形颜色都不同的概率.
思路分析:本题中的基本事件较多,为了清楚地枚举出所有可能的基本事件,可画图枚举如下:

解:本题的基本事件共有27个(如上图).
(1)记“3个矩形都涂同一颜色”为事件A,由图知,事件A的基本事件有3个,故P(A)=![]() =
=![]() .
.
(2)记“3个矩形颜色都不同”为事件B,由图可知,事件B的基本事件有2×3=6个,故P(B)=![]() =
=![]() .
.
答:3个矩形颜色都相同的概率为![]() ,3个矩形颜色都不同的概率为
,3个矩形颜色都不同的概率为![]() .
.
温馨提示
通过树状图或列举法来探求古典概型中的基本事件数,要做到层次分明,不重不漏.

练习册系列答案
相关题目
 用红、黄、蓝三种不同颜色给下图中3个矩形随机涂色,每个矩形只涂一种颜色,求:
用红、黄、蓝三种不同颜色给下图中3个矩形随机涂色,每个矩形只涂一种颜色,求: 用红、黄、蓝三种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,求:
用红、黄、蓝三种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,求: 用红、黄、蓝三种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,求:
用红、黄、蓝三种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,求:
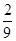 B.
B. C.
C. D.
D.