题目内容
已知圆 :
: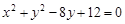 ,直线
,直线 经过点
经过点 ,
,
(1)求以线段 为直径的圆
为直径的圆 的方程;
的方程;
(2)若直线 与圆
与圆 相交于
相交于 ,
,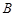 两点,且
两点,且 为等腰直角三角形,求直线
为等腰直角三角形,求直线 的方程.
的方程.
(1)圆 的方程为
的方程为 ;(2)直线
;(2)直线 的方程为:
的方程为: 或
或 .
.
解析试题分析:(1)将圆 化成标准方程,得圆心为
化成标准方程,得圆心为 ,半径为2.从而得到
,半径为2.从而得到 的中点
的中点 ,得所求圆心坐标,再根据两点的距离公式算出半径
,得所求圆心坐标,再根据两点的距离公式算出半径 ,即得以线段
,即得以线段 为直径的圆
为直径的圆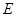 的方程;
的方程;
(2)设直线 的方程为:
的方程为: ,根据题意等腰
,根据题意等腰 中
中 ,利用点到直线的距离公式建立关于
,利用点到直线的距离公式建立关于 的等式,解之可得实数
的等式,解之可得实数 的值,得到直线
的值,得到直线 的方程.
的方程.
试题解析:(1)将圆 的方程
的方程 配方得标准方程为
配方得标准方程为 ,则此圆的圆心为
,则此圆的圆心为 ,半径为2.所以
,半径为2.所以 的中点
的中点 ,可得
,可得 ,所以
,所以 ,即圆
,即圆 的方程为
的方程为 ;
;
设直线 的方程为:
的方程为: ,
, ,且
,且 为等腰直角三角形,
为等腰直角三角形, ,
,
因此圆心 到直线
到直线 的距离
的距离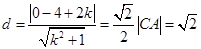
解之得 或
或 ,所求直线
,所求直线 的方程为:
的方程为: 或
或 .
.
考点:圆的标准方程;直线的一般式方程.

练习册系列答案
相关题目
 ,各段弧所在的圆经过同一点
,各段弧所在的圆经过同一点 (点
(点 段弧所对的圆心角为
段弧所对的圆心角为 ,则
,则 ____________ .
____________ .
 上,且过点
上,且过点 、
、 .
. 引切线,切点为Q.试探究:
引切线,切点为Q.试探究: 为定值?若存在,求出点R的坐标;若不存在,请说
为定值?若存在,求出点R的坐标;若不存在,请说 ,求直线l的倾斜角;
,求直线l的倾斜角; =
= ,求此时直线l的方程.
,求此时直线l的方程.
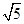 ,求PB的长.
,求PB的长. ,求直线MQ的方程.
,求直线MQ的方程.