题目内容
【题目】设定义在![]() 上的函数
上的函数![]()
![]() ,函数
,函数![]() ,当
,当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,且函数
,且函数![]()
的图象关于点![]() 对称.
对称.
(1)求函数![]() 的表达式;
的表达式;
(2)求证:当![]() 时,
时, 为自然对数的底数);
为自然对数的底数);
(3)若![]() ,数列
,数列![]() 中是否存在
中是否存在![]() ?若存在,求出所有相等的两项,若不存在,说明理由.
?若存在,求出所有相等的两项,若不存在,说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)存在,
;(2)证明见解析;(3)存在,![]()
【解析】
试题分析:(1)函数![]() 的图象关于点
的图象关于点![]() 对称,则函数
对称,则函数![]() 的图象关于点
的图象关于点![]() 对称,即函数
对称,即函数![]() 是奇函数.再结合当
是奇函数.再结合当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,导数为零,可求得
,导数为零,可求得![]() ;(2)由(1)知
;(2)由(1)知![]() 当
当![]() 时不等式
时不等式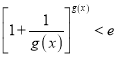 即为:
即为: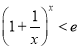 ,等价于
,等价于![]() ,构造函数
,构造函数![]() ,利用导数证明函数
,利用导数证明函数![]() 在
在![]() 上是减函数,故有
上是减函数,故有![]() 时,
时,![]() 成立, 用
成立, 用![]() 代换
代换![]() 得:
得:![]() 时,
时,![]() 成立;(3)依题意
成立;(3)依题意![]() ,利用特殊项可知
,利用特殊项可知![]() ,利用商比较法证明
,利用商比较法证明![]() 的单调性,由此求得
的单调性,由此求得![]() 是唯一结果.
是唯一结果.
试题解析:
(1)将函数![]() 的图象向右平移一个单位,得到函数
的图象向右平移一个单位,得到函数![]() 的图象,
的图象,![]() 函数
函数![]() 的图象关于点
的图象关于点![]() 对称,即函数
对称,即函数![]() 是奇函数,
是奇函数,![]() ,
,
由题意得: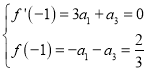 ,所以
,所以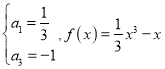 ,经检验满足题意.
,经检验满足题意.
(2)由(1)知![]() 当
当![]() 时不等式
时不等式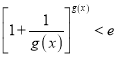 即为:
即为:![]() ,构造函数
,构造函数![]() ,
,
则![]() ,所以函数
,所以函数![]() 在
在![]() 上是减函数, 因而
上是减函数, 因而![]() 时,
时,![]() ,即:
,即:![]() 时,
时,![]() 成立,用
成立,用![]() 代换
代换![]() 得:
得:![]() 时,
时,![]() 成立,所以
成立,所以![]() 时,
时,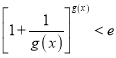 成立.
成立.
(3)![]() ,则由(2)知:
,则由(2)知: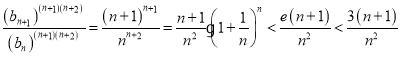 ,
,
令![]() ,得:
,得:![]() ,结合
,结合![]() 得:
得:![]() ,因此,当
,因此,当![]() 时,有
时,有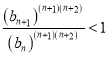 ,所以当
,所以当![]() 时,
时,![]() ,即:
,即:![]() ,又通过比较
,又通过比较![]() 的大小知:
的大小知:![]() ,因为
,因为![]() ,且
,且![]() 时
时![]() ,所以若数列
,所以若数列![]() 中存在相等的两项,只能是
中存在相等的两项,只能是![]() 、
、![]() 与后面的项可能相等,又
与后面的项可能相等,又![]() ,所以数列
,所以数列![]() 中存在唯一相等的两项,即:
中存在唯一相等的两项,即:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第组
人参加“学雷锋”志愿活动,按年龄分组:第组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有人年龄在第
人参加社区宣传交流活动,求至少有人年龄在第![]() 组的概率.
组的概率.
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: .
.