题目内容
【题目】为了保护环境,某工厂在政府部门的支持下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理成本y(万元)与处理量x(吨)之间的函数关系可近似地表示为: ,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
(1)当![]() 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少.
【答案】(1)国家至少需要补贴700万元,该工厂才不会亏损;(2)当处理量为![]() 吨时,每吨的平均处理成本最少.
吨时,每吨的平均处理成本最少.
【解析】
试题(1)利用每处理一吨二氧化碳可得价值为20万元的某种化工产品,及处理成本![]() (万元)与处理量
(万元)与处理量![]() (吨)之间的函数关系,可得利润函数,利用配方法,即可求得结论;(2)求得二氧化碳的每吨平均处理成本函数是分段函数,再分段求出函数的最值,比较其大小,即可求得结论.
(吨)之间的函数关系,可得利润函数,利用配方法,即可求得结论;(2)求得二氧化碳的每吨平均处理成本函数是分段函数,再分段求出函数的最值,比较其大小,即可求得结论.
试题解析:(Ⅰ)当![]() 时,设该工厂获利为
时,设该工厂获利为![]() ,则
,则![]() ,所以当
,所以当![]() 时,
时,![]() ,因此,该工厂不会获利,所以国家至少需要补贴700万元,该工厂才不会亏损; 5分
,因此,该工厂不会获利,所以国家至少需要补贴700万元,该工厂才不会亏损; 5分
(Ⅱ)由题意可知,二氧化碳的每吨平均处理成本为 6分
6分
(1)当![]() 时,
时,![]() ,所以
,所以![]() ,因为
,因为![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() 为减函数;当
为减函数;当![]() 时,
时,![]() ,
,![]() 为增函数,所以当
为增函数,所以当![]() 时,
时,![]() 取得极小值
取得极小值![]() . 9分
. 9分
(2)当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时,
时,![]() 取最小值
取最小值![]() , 12分
, 12分
因为![]() ,所以当处理量为
,所以当处理量为![]() 吨时,每吨的平均处理成本最少. 13分
吨时,每吨的平均处理成本最少. 13分

【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:
(单位:![]() )的影响,对近
)的影响,对近![]() 年的年宣传费
年的年宣传费![]() 和年销售量
和年销售量![]() 作了初步统计和处理,得到的数据如下:
作了初步统计和处理,得到的数据如下:
年宣传费 |
|
|
|
|
年销售量 |
|
|
|
|
![]() ,
,![]() .
.
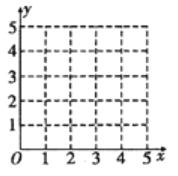
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若公司计划下一年度投入宣传费![]() 万元,试预测年销售量
万元,试预测年销售量![]() 的值.
的值.
参考公式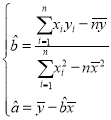
【题目】某公司为了解用户对其产品的满意度,从某地区随机调查了100个用户,得到用户对产品的满意度评分频率分布表如下:
组别 | 分组 | 频数 | 频率 |
第一组 |
| 10 | 0.1 |
第二组 |
| 20 | 0.2 |
第三组 |
| 40 | 0.4 |
第四组 |
| 25 | 0.25 |
第五组 |
| 5 | 0.05 |
合计 | 100 | 1 |
(1)根据上面的频率分布表,估计该地区用户对产品的满意度评分超过70分的概率;
(2)请由频率分布表中数据计算众数、中位数,平均数,根据样本估计总体的思想,若平均分低于75分,视为不满意.判断该地区用户对产品是否满意?
【题目】2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有![]() 人,现采用分层抽样的方法,从该单位上述员工中抽取
人,现采用分层抽样的方法,从该单位上述员工中抽取![]() 人调查专项附加扣除的享受情况.
人调查专项附加扣除的享受情况.
(Ⅰ)应从老、中、青员工中分别抽取多少人?
(Ⅱ)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为![]() .享受情况如右表,其中“
.享受情况如右表,其中“![]() ”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
员工 项目 | A | B | C | D | E | F |
子女教育 | ○ | ○ | × | ○ | × | ○ |
继续教育 | × | × | ○ | × | ○ | ○ |
大病医疗 | × | × | × | ○ | × | × |
住房贷款利息 | ○ | ○ | × | × | ○ | ○ |
住房租金 | × | × | ○ | × | × | × |
赡养老人 | ○ | ○ | × | × | × | ○ |
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件
为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件![]() 发生的概率.
发生的概率.