题目内容
若数列{an}为等差数列,ap=q,aq=p(p≠q),则ap+q为( ).A.p+q B.0 C.-(p+q) D.![]()
解析:法一:∵ap=a1+(p-1)d,aq=a1+(q-1)d,
∴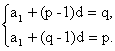
两式相减得(p-q)d=q-p.
∵p≠q,
∴d=-1.
代入得a1=p+q-1.
∴ap+q=a1+(p+q-1)d=p+q-1+(p+q-1)(-1)=0.
∴应选B.
法二:∵ap=aq+(p-q)d,
∴q=p+(p-q)d.
∵p≠q,∴d=-1.
∴ap+q=ap+(p+q-p)d=q+q(-1)=0.
∴应选B.
法三:不防设p<q,由于等差数列中,an关于n的图象是一条直线上均匀排开的一群孤立的点,故三点(p,ap),(q,aq),(p+q,ap+q)共线.设ap+q=m,由已知得三点(p,q),(q,p),(p+q,m)共线(如图).
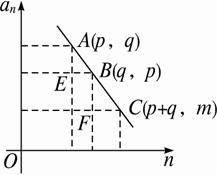
由△ABE∽△BCF,得![]() =
=![]() ,
,
∴![]() =
=![]() .
.
∴![]() =1.
=1.
∴m=0.
∴应选B.
答案:B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 时,
时,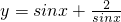 的最小值是
的最小值是 .
. =p(p为常数),则称数列{an}为“等差比”数列,p叫数列{an}的“公差比”.现给出如下命题:
=p(p为常数),则称数列{an}为“等差比”数列,p叫数列{an}的“公差比”.现给出如下命题: