题目内容
10．若函数f（x）=$\sqrt{-{x}^{2}+4x-3}-kx-k+1$有两个零点，则k的取值范围是（ ）| A． | （0，$\frac{1}{2}$] | B． | （$\frac{1}{4}$，$\frac{3}{4}$] | C． | [$\frac{1}{2}$，$\frac{3}{4}$） | D． | [$\frac{1}{4}$，1） |
分析 若函数f（x）=$\sqrt{-{x}^{2}+4x-3}-kx-k+1$有两个零点，则函数y=$\sqrt{-{x}^{2}+4x-3}$与y=kx+k-1的图象有两个交点，数形结合可得答案．
解答 解：若函数f（x）=$\sqrt{-{x}^{2}+4x-3}-kx-k+1$有两个零点，
则函数y=$\sqrt{-{x}^{2}+4x-3}$与y=kx+k-1的图象有两个交点，
函数y=$\sqrt{-{x}^{2}+4x-3}$的图象是以（2，0）点为圆心，半径为1的半圆，
函数y=kx+k-1的图象表示恒过（-1，-1）点的直线，如下图所示：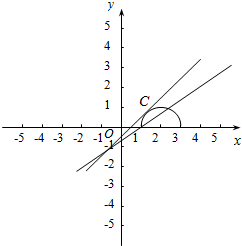
由图可得：函数y=kx+k-1图象过A（1，0）时，k=$\frac{1}{2}$，
函数y=kx+k-1图象与半圆切与C点时，$\frac{|2k+k-1|}{\sqrt{1+{k}^{2}}}=1$，解得：k=$\frac{3}{4}$，或k=0（舍去），
综上可得，k∈[$\frac{1}{2}$，$\frac{3}{4}$），
故选：C
点评 本题考查的知识点是函数的零点，直线与圆的位置关系，难度中档．
练习册系列答案
相关题目
20．如图，执行其程序框图，则输出S的值等于（ ）
| A． | 15 | B． | 105 | C． | 245 | D． | 945 |
1．若直线y=a与函数y=|$\frac{lnx+1}{{x}^{3}}$|的图象恰有3个不同的交点，则实数a的取值范围为（ ）
| A． | {$\frac{{e}^{2}}{3}$} | B． | （0，$\frac{{e}^{2}}{3}$） | C． | （$\frac{{e}^{2}}{3}$，e） | D． | （$\frac{1}{e}$，1）∪{$\frac{{e}^{2}}{3}$} |
15．下列说法正确的是（ ）
| A． | 命题“?x∈R，2x＞0”的否定是“?x0∈R，2${\;}^{{x}_{0}}$＜0” | |
| B． | 命题“若sinx=siny，则x=y”的逆否命题为真命题 | |
| C． | 若命题p，￢q都是真命题，则命题“p∧q”为真命题 | |
| D． | 命题“若△ABC为锐角三角形，则有sinA＞cosB”是真命题 |
2．在用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一周期内的图象时，列表并填入了部分数据，如下表：
（Ⅰ）请将上表空格中处所缺的数据填写在答题卡的相应位置上，并直接写出函数f（x）的解析式；
（Ⅱ）将y=f（x）图象上所有点的横坐标缩短为原来的$\frac{1}{3}$，再将所得图象向左平移$\frac{π}{4}$个单位，得到y=g（x）的图象，求g（x）的单调递增区间．
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{4}$ | π | $\frac{7π}{4}$ | $\frac{5π}{2}$ | $\frac{13π}{4}$ |
| Asin（ωx+φ） | 0 | 3 | 0 | -3 | 0 |
（Ⅱ）将y=f（x）图象上所有点的横坐标缩短为原来的$\frac{1}{3}$，再将所得图象向左平移$\frac{π}{4}$个单位，得到y=g（x）的图象，求g（x）的单调递增区间．